 por LuizCarlos » Ter Ago 16, 2011 15:34
por LuizCarlos » Ter Ago 16, 2011 15:34
Existe alguma maneira de equacionar os problemas ?
Tem problema que eu consigo equacionar, tem outros que eu fico pensando, pensando, pensando e não sei como equacionar !
Estou fazendo uns problemas sobre sistema de equações do 1° grau com duas incognitas, alguns eu consegui equacionar e chegar a solução !
Porem tem dois aqui, que não estou conseguindo !
No Cine Estrela há dois tipos de ingressos: meia entrada e inteira. A meia entrada custa R$ 1,50 e a inteira custa R$ 3,00. No final de uma sessão, o caixa registrou R$ 210,00 para um total de 100 pagantes. Quantas pessoas pagaram ingressos de meia entrada e quantas pagaram ingressos de inteira nessa sessão?
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Neperiano » Ter Ago 16, 2011 19:56
por Neperiano » Ter Ago 16, 2011 19:56
Ola
Não sei se da, mas tente algo assim
f(x) = (x/2).1,50 + x.3
x/2 - meia entrada
x - entrada
Ou usa y no lugar de x
f(x)=(y/2).1,5 + x.3
Coloca 200 no f(x) e resolve por baskara.
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por DanielFerreira » Dom Abr 01, 2012 17:09
por DanielFerreira » Dom Abr 01, 2012 17:09
LuizCarlos escreveu:No Cine Estrela há dois tipos de ingressos: meia entrada e inteira. A meia entrada custa R$ 1,50 e a inteira custa R$ 3,00. No final de uma sessão, o caixa registrou R$ 210,00 para um total de 100 pagantes. Quantas pessoas pagaram ingressos de meia entrada e quantas pagaram ingressos de inteira nessa sessão?
Quantidade de pessoas que pagaram meia entrada: x
Quantidade de pessoas que pagaram inteira: y
CONDIÇÃO I:1,5x + 3y = 210
CONDIÇÃO II:x + y = 100
y = 100 - x
Substituindo II em I:
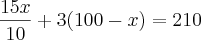

 x = 60
x = 60y = 100 - x
y = 40"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como equacionar essa questão ?
por LuizCarlos » Qua Ago 17, 2011 16:23
- 2 Respostas
- 2439 Exibições
- Última mensagem por LuizCarlos

Qui Ago 18, 2011 14:16
Álgebra Elementar
-
- falta alguma coisa
por johnny » Sex Out 22, 2010 16:57
- 3 Respostas
- 2213 Exibições
- Última mensagem por MarceloFantini

Sex Out 22, 2010 17:23
Cálculo: Limites, Derivadas e Integrais
-
- Expressões tem alguma diferença?
por teilom » Dom Ago 12, 2012 21:34
- 1 Respostas
- 1709 Exibições
- Última mensagem por MarceloFantini

Seg Ago 13, 2012 08:41
Álgebra Elementar
-
- Cálculo de sin(x+y) UMA MANEIRA FÁCIL DE RESOLVER
por Taah » Ter Mar 30, 2010 09:02
- 1 Respostas
- 6523 Exibições
- Última mensagem por paulo87

Sáb Fev 19, 2011 12:26
Desafios Difíceis
-
- Maneira mais eficiente para multiplicacao de fracoes algeb.
por lucas7 » Dom Fev 20, 2011 07:54
- 7 Respostas
- 3896 Exibições
- Última mensagem por lucas7

Seg Fev 21, 2011 16:38
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


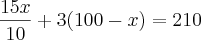





 , avisa que eu resolvo.
, avisa que eu resolvo.

