 por jmoura » Sáb Mar 31, 2012 23:58
por jmoura » Sáb Mar 31, 2012 23:58
Me deparei com uma questão de uma prova antiga que não estou conseguindo resolver:
" Verifique se existe um número real L tal que a função f definida por
f(x)=
![cos\left(\frac{1}{\sqrt[]{x}} \right). sen\left(\frac{\sqrt[]{x+1}-1}{\sqrt[]{x}} \right) cos\left(\frac{1}{\sqrt[]{x}} \right). sen\left(\frac{\sqrt[]{x+1}-1}{\sqrt[]{x}} \right)](/latexrender/pictures/892305de84ef21387bf3e2e208782b9c.png)
, se x>0 e
f(x)= L, se x=0
é contínua no intervalo [0, +

). "
-
jmoura
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Mar 23, 2012 22:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por NMiguel » Dom Abr 01, 2012 08:06
por NMiguel » Dom Abr 01, 2012 08:06

é continua em
![\[[0,+\infty )\] \[[0,+\infty )\]](/latexrender/pictures/b697848248ebb3044e04902ad94130ca.png)
se e só se
![\[f(0)=\lim_{x \to 0}f(x)\] \[f(0)=\lim_{x \to 0}f(x)\]](/latexrender/pictures/72e6d29fe38d7ce2a5f838ddb5bf29ef.png)
, ou seja,
![\[L=\lim_{x \to 0}f(x)\] \[L=\lim_{x \to 0}f(x)\]](/latexrender/pictures/ddc8ec56eed64e87853d096eb414dc95.png)
.
Como

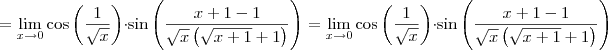

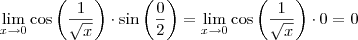
Assim,

é continua em
![\[[0,+\infty )\] \[[0,+\infty )\]](/latexrender/pictures/b697848248ebb3044e04902ad94130ca.png)
se e só se

Editado pela última vez por
NMiguel em Dom Abr 01, 2012 19:14, em um total de 1 vez.
-
NMiguel
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Ter Abr 19, 2011 17:09
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
-
 por NMiguel » Dom Abr 01, 2012 19:13
por NMiguel » Dom Abr 01, 2012 19:13
Sim. De facto é necessário. Sem isso, não poderíamos afirmar que este limite é igual a

. Obrigado pela observação.
Fica então um complemento à resolução.
Sabemos que
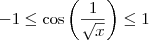
.
Assim,
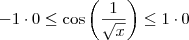
, ou seja,

.
Daqui, sai que
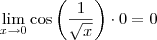
.
Assim, fica completa a demonstração

-
NMiguel
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Ter Abr 19, 2011 17:09
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- como resolver essa questao
por Thassya » Qui Mai 21, 2009 23:25
- 1 Respostas
- 4211 Exibições
- Última mensagem por marciommuniz

Sex Mai 22, 2009 12:23
Trigonometria
-
- Como resolver essa questão da Ufpel?
 por ativirginis » Seg Fev 27, 2012 15:02
por ativirginis » Seg Fev 27, 2012 15:02
- 1 Respostas
- 5178 Exibições
- Última mensagem por LuizAquino

Ter Fev 28, 2012 18:41
Funções
-
- Sem ideia de como resolver essa questão.
por jemourafer » Sáb Abr 28, 2012 00:38
- 1 Respostas
- 1599 Exibições
- Última mensagem por Russman

Sáb Abr 28, 2012 04:52
Cálculo: Limites, Derivadas e Integrais
-
- Como resolver essa questão de probabilidade
por amanda s » Sex Nov 15, 2013 15:11
- 1 Respostas
- 2763 Exibições
- Última mensagem por DanielFerreira

Sex Nov 29, 2013 00:33
Probabilidade
-
- Como resolver essa equação?
por viniciusantonio » Qua Out 21, 2009 19:17
- 1 Respostas
- 4149 Exibições
- Última mensagem por carlos r m oliveira

Qui Out 22, 2009 14:55
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![cos\left(\frac{1}{\sqrt[]{x}} \right). sen\left(\frac{\sqrt[]{x+1}-1}{\sqrt[]{x}} \right) cos\left(\frac{1}{\sqrt[]{x}} \right). sen\left(\frac{\sqrt[]{x+1}-1}{\sqrt[]{x}} \right)](/latexrender/pictures/892305de84ef21387bf3e2e208782b9c.png) , se x>0 e
, se x>0 e  ). "
). "
![cos\left(\frac{1}{\sqrt[]{x}} \right). sen\left(\frac{\sqrt[]{x+1}-1}{\sqrt[]{x}} \right) cos\left(\frac{1}{\sqrt[]{x}} \right). sen\left(\frac{\sqrt[]{x+1}-1}{\sqrt[]{x}} \right)](/latexrender/pictures/892305de84ef21387bf3e2e208782b9c.png) , se x>0 e
, se x>0 e  ). "
). "
 é continua em
é continua em ![\[[0,+\infty )\] \[[0,+\infty )\]](/latexrender/pictures/b697848248ebb3044e04902ad94130ca.png) se e só se
se e só se ![\[f(0)=\lim_{x \to 0}f(x)\] \[f(0)=\lim_{x \to 0}f(x)\]](/latexrender/pictures/72e6d29fe38d7ce2a5f838ddb5bf29ef.png) , ou seja,
, ou seja, ![\[L=\lim_{x \to 0}f(x)\] \[L=\lim_{x \to 0}f(x)\]](/latexrender/pictures/ddc8ec56eed64e87853d096eb414dc95.png) .
.
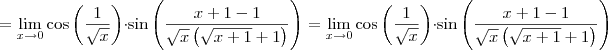

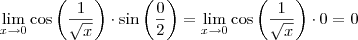
 é continua em
é continua em ![\[[0,+\infty )\] \[[0,+\infty )\]](/latexrender/pictures/b697848248ebb3044e04902ad94130ca.png) se e só se
se e só se 

![cos\left(\frac{1}{\sqrt[]{x}} \right) cos\left(\frac{1}{\sqrt[]{x}} \right)](/latexrender/pictures/0bd3dfe730b93b200c4c64156d0c0c8b.png) é limitada, e aplicar o Teorema do Confronto para provar que o limite é igual a zero?
é limitada, e aplicar o Teorema do Confronto para provar que o limite é igual a zero?
 . Obrigado pela observação.
. Obrigado pela observação.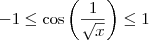 .
.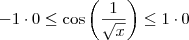 , ou seja,
, ou seja,  .
.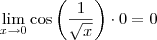 .
.

