 por profmatematica » Qui Mar 29, 2012 13:27
por profmatematica » Qui Mar 29, 2012 13:27
Calcule a derivada de y=x/3x^2+5
eu fiz a derivada aplicando a regra do quociente e encontrei 3x^2-5/ (3x^2+5)^2 pela lógica o resultado teria que simplificar mas todo jeito que faz fico nisso aqui. Alguém pode me auxiliar?
-
profmatematica
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Sex Ago 27, 2010 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Qui Mar 29, 2012 15:05
por LuizAquino » Qui Mar 29, 2012 15:05
profmatematica escreveu:Calcule a derivada de y=x/3x^2+5
Primeiro, o que você escreveu é equivalente a:

Entretanto, ao que parece o exercício original seria:
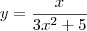
Para escrever algo desse tipo, você deveria ter usado algo como:
y = x/(3x^2 + 5)
Note a importância do uso adequado dos parênteses!
profmatematica escreveu:eu fiz a derivada aplicando a regra do quociente e encontrei 3x^2-5/ (3x^2+5)^2 pela lógica o resultado teria que simplificar mas todo jeito que faz fico nisso aqui. Alguém pode me auxiliar?
Essa não é a reposta correta.
Note que:


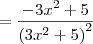
Como não há o que simplificar, a reposta final é:
 Observação
ObservaçãoPor favor, vide a Regra 2 deste fórum:
viewtopic.php?f=9&t=7543
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por profmatematica » Qui Mar 29, 2012 15:11
por profmatematica » Qui Mar 29, 2012 15:11
Valeu mesmo obrigada
-
profmatematica
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Sex Ago 27, 2010 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por profmatematica » Qui Mar 29, 2012 22:22
por profmatematica » Qui Mar 29, 2012 22:22
Luiz a fórmula do quociente não é o contrário? Escreve o primeiro deriva o segundo menos escreve o segundo e deriva o primeiro?
-
profmatematica
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Sex Ago 27, 2010 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por profmatematica » Qui Mar 29, 2012 22:28
por profmatematica » Qui Mar 29, 2012 22:28
gente eu derivei as de quociente tudo ao contrário então misericórdia
-
profmatematica
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Sex Ago 27, 2010 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por profmatematica » Qui Mar 29, 2012 22:33
por profmatematica » Qui Mar 29, 2012 22:33
Gente esse site é o céu Deus abençoe vocês
-
profmatematica
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Sex Ago 27, 2010 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10886 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13191 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14797 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5113 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





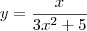


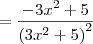









 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.