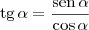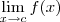por fnolasco » Qua Mar 28, 2012 18:17
por fnolasco » Qua Mar 28, 2012 18:17
-
fnolasco
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Mar 28, 2012 18:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng.Civil
- Andamento: cursando
 por LuizAquino » Qua Mar 28, 2012 19:11
por LuizAquino » Qua Mar 28, 2012 19:11
fnolasco escreveu: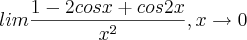
Dica1)

.
2) multiplique o numerador e o denominador por
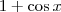
.
fnolasco escreveu: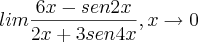
Dica1) Divida o numerador e o denominador por 8x.
fnolasco escreveu:
Dica1) Use a definição de tangente:
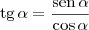 Observação
ObservaçãoPara digitar um limite use um código como:
- Código: Selecionar todos
[tex]\lim_{x\to c} f(x)[/tex]
O resultado desse código é:
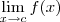
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limites trigonometrico
por caslu13 » Qui Mar 03, 2016 18:07
- 1 Respostas
- 1656 Exibições
- Última mensagem por adauto martins

Sex Mar 04, 2016 12:20
Cálculo: Limites, Derivadas e Integrais
-
- [limites trigonometrico] ajuda urgente
por Rafael eDomus » Qui Set 29, 2011 14:31
- 1 Respostas
- 1039 Exibições
- Última mensagem por Neperiano

Qui Set 29, 2011 16:30
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]: Limite Trigonométrico (cotangente)
 por magalhaesari » Seg Set 08, 2014 15:33
por magalhaesari » Seg Set 08, 2014 15:33
- 0 Respostas
- 1223 Exibições
- Última mensagem por magalhaesari

Seg Set 08, 2014 15:33
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Como calcular esse limite trigonometrico?
por IlgssonBraga » Dom Mar 02, 2014 14:59
- 2 Respostas
- 1988 Exibições
- Última mensagem por IlgssonBraga

Dom Mar 02, 2014 17:01
Cálculo: Limites, Derivadas e Integrais
-
- Círculo trigonométrico
 por Ananda » Sex Fev 29, 2008 10:56
por Ananda » Sex Fev 29, 2008 10:56
- 8 Respostas
- 7528 Exibições
- Última mensagem por Ananda

Seg Mar 03, 2008 17:51
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 13 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
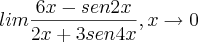


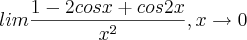
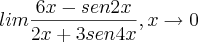


 .
.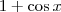 .
.