 por rafaelbr91 » Ter Mar 27, 2012 17:51
por rafaelbr91 » Ter Mar 27, 2012 17:51
Boa tarde! Pessoal estou iniciando o curso de limites e estou com uma duvida, queria saber porque lim sen² x = (lim sen x/x)² quando x->0 . Obrigado!

-
rafaelbr91
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mar 27, 2012 17:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Civil
- Andamento: cursando
 por LuizAquino » Ter Mar 27, 2012 18:25
por LuizAquino » Ter Mar 27, 2012 18:25
rafaelbr91 escreveu:queria saber porque lim sen² x = (lim sen x/x)² quando x->0 .
Esse limites não são iguais.
Os limites que são iguais seriam:
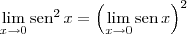
Note que podemos fazer o seguinte desenvolvimento:
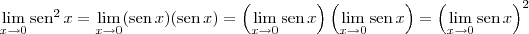
rafaelbr91 escreveu:Pessoal estou iniciando o curso de limites
Se desejar assistir videoaulas sobre esse assunto, então eu gostaria de recomendar o meu canal no YouTube:
http://www.youtube.com/LCMAquinoEu espero que as videoaulas em meu canal possam lhe ajudar nos seus estudos.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por rafaelbr91 » Ter Mar 27, 2012 18:43
por rafaelbr91 » Ter Mar 27, 2012 18:43
Pois é! Por isso que achei estranho quando vi essa "igualdade". Obrigado! E quanto ao seu canal, eu ja assisti todos videos de limites dele, estou no 1º de derivada nesse exato momento, que coincidência!kkkkkkkkkkkkkk Obrigado!
-
rafaelbr91
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mar 27, 2012 17:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite de uma função trigonométrica
por Douglas16 » Seg Mar 11, 2013 14:45
- 1 Respostas
- 1390 Exibições
- Última mensagem por Douglas16

Seg Mar 11, 2013 15:32
Cálculo: Limites, Derivadas e Integrais
-
- Limite de uma função trigonométrica
por Douglas16 » Sáb Mar 16, 2013 21:52
- 3 Respostas
- 2225 Exibições
- Última mensagem por e8group

Dom Mar 17, 2013 00:34
Cálculo: Limites, Derivadas e Integrais
-
- Limite de função trigonométrica
por Carolminera » Qui Jul 17, 2014 15:44
- 4 Respostas
- 2992 Exibições
- Última mensagem por Carolminera

Dom Jul 20, 2014 21:52
Cálculo: Limites, Derivadas e Integrais
-
- Limite de função trigonométrica
por Fernandobertolaccini » Qua Jul 30, 2014 23:27
- 1 Respostas
- 2695 Exibições
- Última mensagem por Man Utd

Qui Ago 07, 2014 15:37
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda com limite de função trigonométrica
por sofa » Qua Jun 29, 2011 04:42
- 6 Respostas
- 3613 Exibições
- Última mensagem por sofa

Qua Jun 29, 2011 06:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



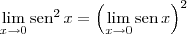
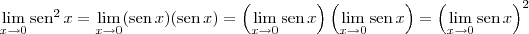


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.