 por Aninha Mendes » Seg Mar 26, 2012 17:36
por Aninha Mendes » Seg Mar 26, 2012 17:36
Olá... eu sei que o exercício é meio besta, mas eu realmente preciso de ajuda.
A idade de Paulo é o dobro da idade de Marcel. Há dez anos, a idade de Paulo era o quadruplo da idade de Marcel. A soma das idades atuais de Paulo e Marcel, em anos, é?
Eu tentei assim: M = 2xP
M = 4x P - 10
Eu não sei o que fazer. Desde já agradeço.

-
Aninha Mendes
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Fev 06, 2012 19:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Seg Mar 26, 2012 18:11
por MarceloFantini » Seg Mar 26, 2012 18:11
Você está interpretando errado o exercício. Note que o que você escreveu foi que a idade de Marcel era o dobro da de Paulo (

) e depois que Marcel tem quatro vezes a idade de Paulo menos 10 anos (
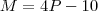
).
Se Paulo tem o dobro da idade de Marcel, então

.
Se há dez anos a idade de Paulo era o quádruplo da idade de Marcel, então

.
Tente resolver agora.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LÓGICA] simplificação lógica e leis de equivalência
por MatheusComp606 » Qua Ago 24, 2016 16:13
- 1 Respostas
- 5801 Exibições
- Última mensagem por adauto martins

Seg Ago 29, 2016 15:34
Lógica
-
- [Função] isso é função do segundo grau?
por maulakalanata » Qua Mar 27, 2013 04:03
- 1 Respostas
- 2286 Exibições
- Última mensagem por timoteo

Qua Mar 27, 2013 10:51
Funções
-
- [Função 1°grau] determinar função.
por Thiago 86 » Ter Abr 23, 2013 11:27
- 2 Respostas
- 2412 Exibições
- Última mensagem por Thiago 86

Ter Abr 23, 2013 13:05
Funções
-
- Função do 2° Grau
por mimi2009 » Qua Jun 10, 2009 05:46
- 1 Respostas
- 2088 Exibições
- Última mensagem por Molina

Qua Jun 10, 2009 08:05
Funções
-
- Função do 2 grau...
por Fiel8 » Qua Jul 01, 2009 21:34
- 4 Respostas
- 3441 Exibições
- Última mensagem por Cleyson007

Qui Jul 02, 2009 16:16
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ) e depois que Marcel tem quatro vezes a idade de Paulo menos 10 anos (
) e depois que Marcel tem quatro vezes a idade de Paulo menos 10 anos (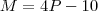 ).
). .
. .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.