Livia000 escreveu:Alguém poderia me ajudar nesta questão?
limx>1+(pela direita) = [ 1/?(x²-1) - 1/?((x^3) - 1) ]
Primeiro, antes de postar um tópico leia as Regras deste fórum:
viewtopic.php?f=9&t=7543Em especial, vide a regra 2.
Livia000 escreveu:limx>1+(pela direita) = [ 1/?(x²-1) - 1/?((x^3) - 1) ]
Tentei resolvê-la utilizando a ideia de derivada :
limx>1+(pela direita) = [ 1/?(x²-1) - 1/?((x^3) - 1) ] = limx>1+[ ?(x²-1)/(x+1)/(x-1)] + limx>1+ [ ?(x^3-1)/(x² + x + 1)/(x - 1)] =
limites esses que são iguais às derivadas das funções ?(x²-1)/(x+1) em x= 1 e ?(x^3-1)/( x²+x+1) em x=1 ; respectivamente...
mas, é certo fazer desse jeito, uma vez que não sabemos se o limite de f(x) - f(1)/x-1 qdo x>1 (tende a 1) existe para as duas funções?
Para qualquer que seja a função real f(x), se 1 é um ponto tal que
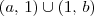
faz parte do domínio de f, então temos que sempre existem os seguintes limites laterais:

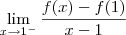
Os resultados desses limites podem ser um número real fixo ou ainda infinito.
Além disso, se os resultados desses dois limites laterais forem distintos, então não existirá o limite "geral":
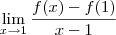
De qualquer modo, não é necessário utilizar o conceito de derivadas nesse exercício. Vejamos a resolução.
Temos o seguinte limite:
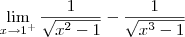
Note que:

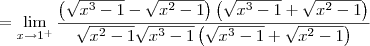

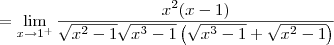

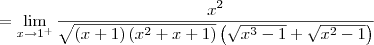
Note que o numerador se aproxima de 1 (pela direita). Já o denominador se aproxima de 0 (pela direita). Desse modo, esse limite é igual a

.
Em resumo, temos então que:
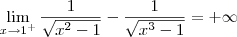


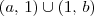 faz parte do domínio de f, então temos que sempre existem os seguintes limites laterais:
faz parte do domínio de f, então temos que sempre existem os seguintes limites laterais:
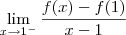
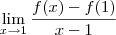
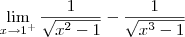

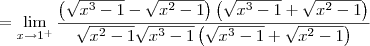

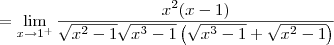

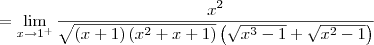
 .
.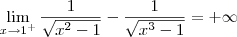

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.