1-Determine o valor da constante C para que F seja continua em [0,
 )
)![f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1 f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1](/latexrender/pictures/39e46eb54f0ef49ad0383fcd1334a2c1.png)

<=,=> Querem dizer maior ou igual
Bom, a minha dúvida é a seguinte: No primeiro momento, eu igualei a f(x)

substituio x por 1para achar f(1), porem quando vo fazer o limite da
![f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1 f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1](/latexrender/pictures/39e46eb54f0ef49ad0383fcd1334a2c1.png)
com X tendendo a 1, caio numa indeterminação 0/0. Minha idéia era achar o valor do limite
![f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1 f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1](/latexrender/pictures/39e46eb54f0ef49ad0383fcd1334a2c1.png) com X tendendo a 1 e dps igualar a F(1) para achar o C
com X tendendo a 1 e dps igualar a F(1) para achar o CQueria saber se o meu pensamento está correto e como sair da indeterminação
Obrigado


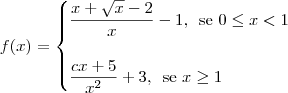

 , se 0<= x <1
, se 0<= x <1 , se x =>1
, se x =>1


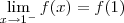
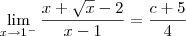
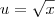 . Desse modo, quando
. Desse modo, quando  temos que
temos que  . Podemos então reescrever esse limite como:
. Podemos então reescrever esse limite como:





 .
.
 :
: