 por shyzum » Qua Mar 21, 2012 18:07
por shyzum » Qua Mar 21, 2012 18:07
encontrei o seguinte exercício que eu não consigo fazer de jeito nenhum, por favor alguem me ajude

-
shyzum
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Mar 11, 2012 18:22
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia
- Andamento: cursando
 por TAE » Qua Mar 21, 2012 20:51
por TAE » Qua Mar 21, 2012 20:51
...
“O tolo, quando erra,queixa-se dos outros; o sábio queixa-se de si mesmo.” (Sócrates, 469-399, AC).
-
TAE
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Mar 20, 2012 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: TÉC. ELETRÔNICA
- Andamento: formado
 por Zetsu PN » Seg Abr 02, 2012 23:14
por Zetsu PN » Seg Abr 02, 2012 23:14
| x² - 1 | < x
Analisando o primeiro membro temos que:
| x² - 1 | = x² - 1 <=>
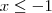
ou

| x² - 1 | = 1 - x² <=>

Para qualquer valor real de x elemento do intervalo [-1,1] a inequação será válida. Deve-se alisar, pois, para os valores do intervalos
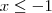
ou

x² - x - 1 < 0
(delta) = 1 + 4 = 5
x' =
![\frac{(1 + \sqrt[2]{5} )}{2} \frac{(1 + \sqrt[2]{5} )}{2}](/latexrender/pictures/fd54137b121406ab2c886791018cd4c8.png)
x" =
![\frac{(1 - \sqrt[2]{5} )}{2} \frac{(1 - \sqrt[2]{5} )}{2}](/latexrender/pictures/85b8b071ae4c51e9c0bad59e3d04b357.png)
Portanto, a solução da inequação será o valor negativo de y, ou seja, o interior das raízes. Sendo assim:
S = { x e R |
![\frac{(1 + \sqrt[2]{5} )}{2} \frac{(1 + \sqrt[2]{5} )}{2}](/latexrender/pictures/fd54137b121406ab2c886791018cd4c8.png)
< x <
![\frac{(1 - \sqrt[2]{5} )}{2} \frac{(1 - \sqrt[2]{5} )}{2}](/latexrender/pictures/85b8b071ae4c51e9c0bad59e3d04b357.png)
}
(Sou novo no fórum e usei o site
http://www.ajudamatematica.com/equationeditor/ para formular. Fui didático?

)
Editado pela última vez por
Zetsu PN em Seg Abr 02, 2012 23:41, em um total de 1 vez.
-
Zetsu PN
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Abr 02, 2012 22:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Abr 02, 2012 23:32
por MarceloFantini » Seg Abr 02, 2012 23:32
Falta apenas escrever [ tex] e [/ tex] sem o espaço entre as fórmulas para que o fórum transforme-as em imagens.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Inequação Modular] Alguém por favor me ajuda nessa questão?
por FuturoFuturista » Ter Jan 22, 2013 21:27
- 1 Respostas
- 2641 Exibições
- Última mensagem por e8group

Ter Jan 22, 2013 22:15
Inequações
-
- [Ajuda] Inequação modular
por wallsoares » Seg Mar 21, 2011 19:57
- 1 Respostas
- 1374 Exibições
- Última mensagem por Elcioschin

Seg Mar 21, 2011 20:14
Álgebra Elementar
-
- n sei resolver essa funçao modular com inequaçao(ajuda)
por Fabricio dalla » Qua Mar 09, 2011 23:46
- 4 Respostas
- 3273 Exibições
- Última mensagem por Renato_RJ

Sex Mar 11, 2011 15:00
Funções
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7384 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- inequação modular
por manuoliveira » Dom Ago 22, 2010 22:30
- 1 Respostas
- 3469 Exibições
- Última mensagem por Dan

Seg Ago 23, 2010 15:38
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






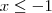 ou
ou 

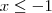 ou
ou 
![\frac{(1 + \sqrt[2]{5} )}{2} \frac{(1 + \sqrt[2]{5} )}{2}](/latexrender/pictures/fd54137b121406ab2c886791018cd4c8.png)
![\frac{(1 - \sqrt[2]{5} )}{2} \frac{(1 - \sqrt[2]{5} )}{2}](/latexrender/pictures/85b8b071ae4c51e9c0bad59e3d04b357.png)
![\frac{(1 + \sqrt[2]{5} )}{2} \frac{(1 + \sqrt[2]{5} )}{2}](/latexrender/pictures/fd54137b121406ab2c886791018cd4c8.png) < x <
< x < ![\frac{(1 - \sqrt[2]{5} )}{2} \frac{(1 - \sqrt[2]{5} )}{2}](/latexrender/pictures/85b8b071ae4c51e9c0bad59e3d04b357.png) }
} )
)

