Pessoal gostaria de pedir a ajuda de voçes para analizar se está certo ou não? Obrigado e fiquem com Deus
De uma longa folha retangular de metal, com 30cm de largura, deve-se fazer uma calha, dobrando as bordas perpendicularmente a folha. quantos centimetros devem se dobrados, de cada lado, de modo que a calha venha a ter capacidade maxima. Gostaria de saber se esta minha resolução está certa caso contrario peço ajuda.
Resolução: f(x)= x(30-2x)
f(x)= -2x²+30x
f'(x)=-4x+30
f''(x)= x=30/4=7,5
Teste para x=7,5 na derivada de 2°ordem f''(x)
f''(7.5)= 7,5<0
fmaximo= f(7,5)= 2(7,5)^2 + 30(7,5)
= 30+225=255
fmaximo=255



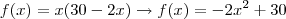
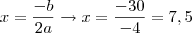


 .
.
 :
: