Pri Ferreira escreveu:Considere-se o conjunto A = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11;
12; 13; 14}, formado pelos quatorze primeiros inteiros positivos,
e um conjunto B, formado por todos os subconjuntos
de A com exatamente três elementos. Escolhendo-se
aleatoriamente um elemento do conjunto B, a probabilidade
de ele ser formado por três números cuja soma é um múltiplo
de 3 equivale a:
a)168/17
b)4/31
c)1/13
d)31/91
Note que cada
elemento do conjunto B tem o formato {a, b, c}.
Note também que o número de elementos de B será
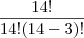
.
Agora você precisa listar todos os elementos de B que são formados por três números cuja a soma é um múltiplo de 3. Veja alguns exemplos: {1, 2, 3}, {1, 2, 6}, {1, 3, 5}, etc.
Depois que você contar quantos elementos tem nessa listagem, basta calcular a probabilidade solicitada no exercício.


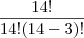 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.