Uma equação vetorial da reta que passa em P (-1,2,3) e é perpendicular ao plano
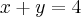 é:
é:(A)

(B)
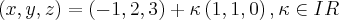
(C)

(D)


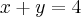 é:
é:
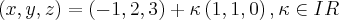



rola09 escreveu:Uma equação vetorial da reta que passa em P (-1,2,3) e é perpendicular ao planoé:
(A)
(B)
(C)
(D)
rola09 escreveu:Alguém me poderia ajudar a resolver este exercício. Penso que o objetivo passe por experimentar os sistemas, mas estou um pouco confuso.
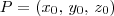 e tem vetor diretor
e tem vetor diretor  , é dada por:
, é dada por:



Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.



