rola09 escreveu:Considere a recta r de equação:

e o ponto P (1,1,1).
rola09 escreveu:NOTA: não consegui descobrir como faço a fórmula de dividir. Na equação o 2 é denominador de x-1 e o 3 é denominador de y-3.
Basta usar o comando "\frac{}{}". Por exemplo, o código ficaria assim:
- Código: Selecionar todos
[tex]\frac{x - 1}{2} = \frac{y-3}{3}[/tex]
O resultado desse código será:
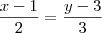
rola09 escreveu:- Indique um ponto da recta dada e um vector com a sua direcção.
Primeiro, todos os pontos dessa reta tem coordenada z igual a 0.
Agora, atribua um valor para x e calcule qual será o valor de y.
Por exemplo, atribuindo x = 1, temos que y = 3.
Sendo assim, um ponto dessa reta é (1, 3, 0).
Para determinar um vetor com mesma direção de r, você precisa determinar outro ponto de r. Por exemplo, temos o ponto (3, 6, 0).
Desse modo, um vetor com mesma direção de r será dado por:
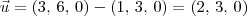
rola09 escreveu:- Determine as equações cartesianas da recta que contém P e é paralela á recta r.
Não há "equação cartesiana" para uma reta que esteja no espaço. O que podemos exibir é uma equação paramétrica ou ainda uma equação vetorial.
Se a reta s é paralela à r, então ela possui o mesmo vetor diretor da reta r. Por exemplo, o vetor
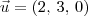
é um vetor diretor de s.
Portanto, uma equação paramétrica para s será dada por:
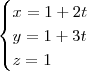
rola09 escreveu:- Escreva a equação do plano que contém P e é perpendicular a r.
Se a reta r é perpendicular ao plano

, então o vetor diretor da reta r é um vetor normal do plano

. Por exemplo, o vetor
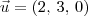
é um vetor normal de

.
Portanto, a equação do plano

será dada por:
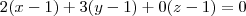
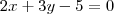
rola09 escreveu:- Determine a de forma que
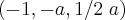
seja ponto da recta.
Você já sabe que todos os pontos da reta r possuem coordenada z igual a 0.
Sendo assim, devemos ter
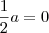
. Ou seja,

.
Agora verifique que o ponto (-1, 0, 0) de fato pertence a reta r.
 e o ponto P (1,1,1).
e o ponto P (1,1,1).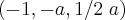 seja ponto da recta.
seja ponto da recta.

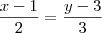
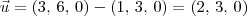
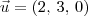 é um vetor diretor de s.
é um vetor diretor de s. 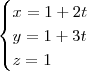
 , então o vetor diretor da reta r é um vetor normal do plano
, então o vetor diretor da reta r é um vetor normal do plano 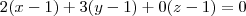
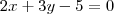
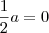 . Ou seja,
. Ou seja,  .
.
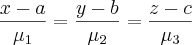
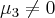 certo?
certo? então
então 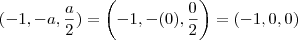 .
.
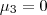 (note que você escreveu errado, pois disse que
(note que você escreveu errado, pois disse que 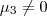 ) .
) .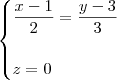
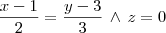
 (que é o conectivo lógico de conjunção) para indicar que os pontos da reta atendem ao mesmo tempo as duas equações.
(que é o conectivo lógico de conjunção) para indicar que os pontos da reta atendem ao mesmo tempo as duas equações.
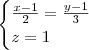


 , avisa que eu resolvo.
, avisa que eu resolvo.

