por cal12 » Sex Mar 16, 2012 18:38
galera voces poderiam me esplicar como é que se esboça o grafico da funcao em limites pois eu não sei como se faz para esboça o grafico, eu so sei analisar.
pode ser postando algum video para eu estudar eu ezplicando alguma função.
-
cal12
- Novo Usuário
-
- Mensagens: 8
- Registrado em: Dom Ago 14, 2011 11:21
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
por LuizAquino » Sex Mar 16, 2012 19:16
cal12 escreveu:galera voces poderiam me esplicar como é que se esboça o grafico da funcao em limites pois eu não sei como se faz para esboça o grafico, eu so sei analisar.
Você se refere a traçar o esboço do gráfico de uma função apenas analisando o limite dessa função em alguns pontos?
Se for isso, na verdade você deseja traçar o gráfico de funções racionais, isto é, funções do tipo:
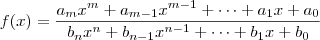
Para traçar o esboço do gráfico de funções desse tipo, você precisa determinar as assíntotas horizontais e as assíntotas verticais.
-
LuizAquino
- Colaborador Moderador - Professor
-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Gráfico.
por Josiebruno » Seg Out 18, 2010 18:47
- 3 Respostas
- 2976 Exibições
- Última mensagem por Josiebruno
Ter Out 19, 2010 12:24
Funções
-
- gráfico
por Andreza » Qui Nov 24, 2011 13:23
- 0 Respostas
- 1436 Exibições
- Última mensagem por Andreza
Qui Nov 24, 2011 13:23
Funções
-
- Grafico
por bruno ken taniwaki » Dom Fev 24, 2013 14:36
- 0 Respostas
- 1146 Exibições
- Última mensagem por bruno ken taniwaki
Dom Fev 24, 2013 14:36
Cálculo: Limites, Derivadas e Integrais
-
- gráfico
por Jhennyfer » Seg Mai 20, 2013 08:34
- 0 Respostas
- 1135 Exibições
- Última mensagem por Jhennyfer
Seg Mai 20, 2013 08:34
Funções
-
- Gráfico com f(x)=cos.x?
por Paulo Ricardo » Qua Ago 14, 2013 03:24
- 1 Respostas
- 1652 Exibições
- Última mensagem por Russman
Qua Ago 14, 2013 21:04
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {
} e B = {
}, então o número de elementos A
B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
