 por Pri Ferreira » Qui Mar 15, 2012 17:22
por Pri Ferreira » Qui Mar 15, 2012 17:22
O resultado da simplificação da expressão 7^9+4X7^6+5X7^3+2/344² é
a) 7³ + 2
b)7³ - 4
c)7³ + 5
d) 3
e) 1
Já tentei várias vezes naum sei se tem alguma coisa errada na questão ou algum passo q ainda naum visualizei. Ajudem!!!
-
Pri Ferreira
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Qua Out 19, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por LuizAquino » Sex Mar 16, 2012 12:49
por LuizAquino » Sex Mar 16, 2012 12:49
Pri Ferreira escreveu:O resultado da simplificação da expressão 7^9+4X7^6+5X7^3+2/344² é
a) 7³ + 2
b)7³ - 4
c)7³ + 5
d) 3
e) 1
Pri Ferreira escreveu:Já tentei várias vezes naum sei se tem alguma coisa errada na questão ou algum passo q ainda naum visualizei.
A expressão que você escreveu no exercício é equivalente equivalente a:
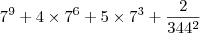
Entretanto, ao que parece a expressão original do exercício seria:

Para escrever essa expressão, você deveria ter usado algo do tipo:
(7^9 + 4*7^6 + 5*7^3 + 2)/(344^2)
Note a importância do uso adequado dos parênteses!
Vejamos agora os passos para a resolução do exercício.
Note que:
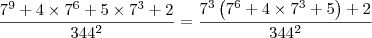
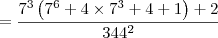
![= \dfrac{7^3\left[ (7^3 + 2)^2 + 1\right] + 2}{344^2} = \dfrac{7^3\left[ (7^3 + 2)^2 + 1\right] + 2}{344^2}](/latexrender/pictures/e3321cc1381e1676b6c4602f7b791595.png)

![= \dfrac{\left(7^3 + 2\right)\left[7^3\left(7^3 + 2\right) + 1\right]}{344^2} = \dfrac{\left(7^3 + 2\right)\left[7^3\left(7^3 + 2\right) + 1\right]}{344^2}](/latexrender/pictures/3e6162b472d180bb38edf3e0c11deb7e.png)
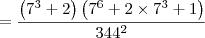
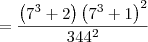

 Observação
ObservaçãoPara digitar os símbolos e notações matemáticas de forma conveniente, por favor leia o tópico abaixo:
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Simplicação de Expressão
por mayaracalixta » Dom Fev 21, 2016 04:29
- 1 Respostas
- 1536 Exibições
- Última mensagem por DanielFerreira

Seg Fev 22, 2016 20:40
Polinômios
-
- Simplicação trabalhando expoentes.
por Rafael Sposito » Dom Fev 17, 2013 17:51
- 1 Respostas
- 1452 Exibições
- Última mensagem por young_jedi

Dom Fev 17, 2013 23:47
Álgebra Elementar
-
- [Séries] Sobre simplicação de expressões em séries
por HenriqueOrlan » Sáb Nov 21, 2015 11:28
- 1 Respostas
- 3727 Exibições
- Última mensagem por adauto martins

Qua Nov 25, 2015 16:31
Sequências
-
- Expressão
por geriane » Qui Abr 22, 2010 12:49
- 4 Respostas
- 3885 Exibições
- Última mensagem por geriane

Sáb Abr 24, 2010 10:50
Trigonometria
-
- Expressão em PG
por Carolziiinhaaah » Qua Jun 16, 2010 21:10
- 1 Respostas
- 2006 Exibições
- Última mensagem por MarceloFantini

Qua Jun 16, 2010 21:39
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



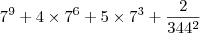

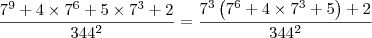
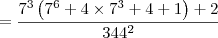
![= \dfrac{7^3\left[ (7^3 + 2)^2 + 1\right] + 2}{344^2} = \dfrac{7^3\left[ (7^3 + 2)^2 + 1\right] + 2}{344^2}](/latexrender/pictures/e3321cc1381e1676b6c4602f7b791595.png)

![= \dfrac{\left(7^3 + 2\right)\left[7^3\left(7^3 + 2\right) + 1\right]}{344^2} = \dfrac{\left(7^3 + 2\right)\left[7^3\left(7^3 + 2\right) + 1\right]}{344^2}](/latexrender/pictures/3e6162b472d180bb38edf3e0c11deb7e.png)
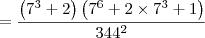
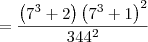



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
