 por ViniRFB » Sex Mar 09, 2012 18:28
por ViniRFB » Sex Mar 09, 2012 18:28
Se
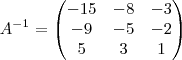
, e
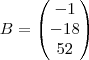
resolva a equação matricial AX = B
Sei que temos que encontrar X, mas não temos A.
Pela resolução ficou assim:
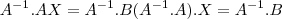
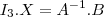

Logo não precisamos achar a matriz A.
queria que alguém me ensinasse esse passo a passo da equação, por favor.
grato
ViniRFB
Editado pela última vez por
ViniRFB em Sex Mar 09, 2012 20:15, em um total de 2 vezes.
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ViniRFB » Sex Mar 09, 2012 19:23
por ViniRFB » Sex Mar 09, 2012 19:23
Pessoal como me saio desta?
Matriz A =
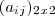
tal que A =

como encontro o valor?
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ViniRFB » Sex Mar 09, 2012 19:52
por ViniRFB » Sex Mar 09, 2012 19:52
ViniRFB escreveu:Pessoal como me saio desta?
Matriz A =
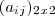
tal que A =

como encontro o valor?
Já sei como resolver. Amigos peguem as correspondestes, ou seja, quando a matriz for dada temos que ter em mente o seguinte:
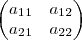
então resolve-se pela matriz que foi dada.
Resultado é

Valeu
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Sex Mar 09, 2012 20:03
por MarceloFantini » Sex Mar 09, 2012 20:03
Vini, não consigo entender a primeira questão. Na primeira você explicitou A e algum tempo depois diz que "A não foi dada".
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ViniRFB » Sex Mar 09, 2012 20:15
por ViniRFB » Sex Mar 09, 2012 20:15
Olá, Fantini.
Então eu errei agora arrumei lá.
Desculpe-me!
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinar a matriz X na Equação matricial AX=B
por hugo guedes » Qui Mar 12, 2015 10:37
- 1 Respostas
- 24049 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 25, 2015 16:58
Matrizes e Determinantes
-
- Determinar a matriz X na Equação matricial AX=B
por hugo guedes » Qui Mar 12, 2015 12:16
- 1 Respostas
- 4380 Exibições
- Última mensagem por andrerodrigues98

Qui Mar 12, 2015 15:25
Matrizes e Determinantes
-
- [Equação matricial envolvendo matriz inversa] Como isolar X?
por Mario_Mascarenhas » Sáb Mar 22, 2014 17:52
- 1 Respostas
- 3341 Exibições
- Última mensagem por e8group

Seg Mar 24, 2014 01:12
Álgebra Linear
-
- [Equação matricial envolvendo matriz inversa] Como isolar X?
por Mario_Mascarenhas » Sáb Mar 22, 2014 17:52
- 0 Respostas
- 1768 Exibições
- Última mensagem por Mario_Mascarenhas

Sáb Mar 22, 2014 17:52
Álgebra Linear
-
- Equação matricial
por SAAMS » Dom Nov 28, 2010 17:18
- 0 Respostas
- 3683 Exibições
- Última mensagem por SAAMS

Dom Nov 28, 2010 17:18
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
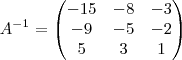 , e
, e 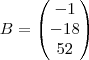
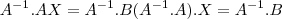
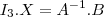


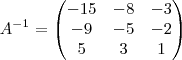 , e
, e 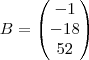
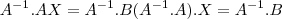
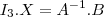


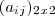 tal que A =
tal que A =  como encontro o valor?
como encontro o valor?
tal que A =
como encontro o valor?
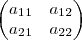 então resolve-se pela matriz que foi dada.
então resolve-se pela matriz que foi dada. 



