Resolvi a seguinte inequação, mas a resposta está errada de acordo com meu livro:
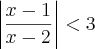
1ª inequação
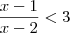
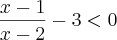
Resolvendo isso, ficou assim:

Depois disso, tirei a raiz do numerador e do denominador para ver quais valores de x satisfaz essa inequação.
Agora resolvendo:
2ª inequação

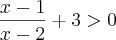
dando:

Depois disso, tirei a raiz do numerador e do denominador para ver quais valores de x satisfaz essa inequação.
Depois de ter tirado as raízes das duas inequações, joguei na reta a 1ª inequação para saber os valores de x para que a inequação seja menor que 0, e fazendo o mesmo para a 2ª inequação, só que dessa vez para achar os valores de x para que seja maior que 0.
E em seguida, coloquei as retas das duas inequações paralelas para fazer a intersecção para achar os valores de x para satisfazer as duas inequações.
E minha resposta foi:
S = {x ? ?|
 ou
ou 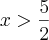
A resposta do meu livro é:
S = {x ? ?|
 ou
ou  }
}Valeu gente!


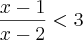
 (o que significa que
(o que significa que 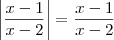 ). Desse modo, você tem um sistema de inequações:
). Desse modo, você tem um sistema de inequações: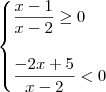
 .
. (o que significa que
(o que significa que  ). Desse modo, você tem um sistema de inequações:
). Desse modo, você tem um sistema de inequações:
 .
.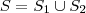 .
.



 , avisa que eu resolvo.
, avisa que eu resolvo.

