 por Fabricio dalla » Qua Mar 07, 2012 12:54
por Fabricio dalla » Qua Mar 07, 2012 12:54
alguem pode me explicar direito o teorema de bolzano chegui a olhar em um livro e a procurar no site e n entendi muito bem
desde ja agradeço!
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qua Mar 07, 2012 19:16
por MarceloFantini » Qua Mar 07, 2012 19:16
O teorema de Bolzano diz o seguinte:
Dada uma função contínua

num intervalo fechado
![[a,b] [a,b]](/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png)
, tal que
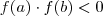
, então existe um
![c \in [a,b] c \in [a,b]](/latexrender/pictures/89a48a2849559c11ee668929aa8a973f.png)
tal que
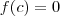
.
Vamos interpretá-lo. Se a função é contínua, então não tem saltos, pontos faltando, etc. Intuitivamente, você pode desenhar o gráfico sem tirar o lápis do papel. A condição de que
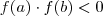
significa que ela muda de sinal, ou seja, ela pode ser positiva e passar a ser negativa ou negativa e passa a ser positiva. A conclusão é que se isto acontece, a função tem uma raíz neste intervalo para algum ponto.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exercício com Teorema de Bolzano
por fff » Qua Fev 05, 2014 11:54
- 4 Respostas
- 1949 Exibições
- Última mensagem por fff

Qui Fev 06, 2014 17:19
Cálculo: Limites, Derivadas e Integrais
-
- Método da Bissecção Teorema de Bolzano
por romulo39 » Qua Out 12, 2011 00:05
- 1 Respostas
- 1833 Exibições
- Última mensagem por LuizAquino

Qua Out 12, 2011 09:14
Cálculo: Limites, Derivadas e Integrais
-
- Teorema das linhas
por valleska » Seg Mai 18, 2009 21:46
- 1 Respostas
- 3255 Exibições
- Última mensagem por Guill

Dom Jul 10, 2011 11:20
Desafios Enviados
-
- teorema de pitagoras
por stanley tiago » Sex Jan 21, 2011 15:59
- 5 Respostas
- 4663 Exibições
- Última mensagem por stanley tiago

Sáb Jan 22, 2011 15:49
Geometria Analítica
-
- teorema de pitagoras
por stanley tiago » Dom Fev 13, 2011 18:35
- 4 Respostas
- 3496 Exibições
- Última mensagem por stanley tiago

Seg Fev 14, 2011 22:00
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 num intervalo fechado
num intervalo fechado ![[a,b] [a,b]](/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) , tal que
, tal que 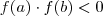 , então existe um
, então existe um ![c \in [a,b] c \in [a,b]](/latexrender/pictures/89a48a2849559c11ee668929aa8a973f.png) tal que
tal que 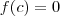 .
. 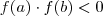 significa que ela muda de sinal, ou seja, ela pode ser positiva e passar a ser negativa ou negativa e passa a ser positiva. A conclusão é que se isto acontece, a função tem uma raíz neste intervalo para algum ponto.
significa que ela muda de sinal, ou seja, ela pode ser positiva e passar a ser negativa ou negativa e passa a ser positiva. A conclusão é que se isto acontece, a função tem uma raíz neste intervalo para algum ponto.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
