por sony01 » Seg Mar 05, 2012 21:39
por sony01 » Seg Mar 05, 2012 21:39
Analise as seguintes afirmações:
I - Se x e y são números reais positivos então
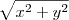
=

.
II - Para quaisquer números reais x e y, tem-se

.
III - A igualdade

vale para quaisquer números reais não nulos x e y.
IV - Se x é um número real tal que
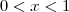
então

Pode-se dizer que:
a) Apenas uma afirmação é verdadeira.
b) Apenas duas afirmações são verdadeiras.
c) Apenas três afirmações são verdadeiras.
d) Todas as afirmações são verdadeiras.
CálculoI - Se x e y são números reais positivos então 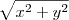 =
=  .
.![\displaystyle \sqrt[2]{x^2+y^2} = \sqrt[\not 2]{x^{ \not 2}} + \sqrt[ \not 2]{y^{ \not 2}} = x + y \displaystyle \sqrt[2]{x^2+y^2} = \sqrt[\not 2]{x^{ \not 2}} + \sqrt[ \not 2]{y^{ \not 2}} = x + y](/latexrender/pictures/b72c6a7039de78fa463d388da31963a1.png) 1ª Afirmação Verdadeira.II - Para quaisquer números reais x e y, tem-se
1ª Afirmação Verdadeira.II - Para quaisquer números reais x e y, tem-se  .
.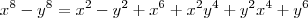
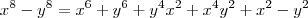
Logo,
 2ª Afirmação Falsa.III - A igualdade
2ª Afirmação Falsa.III - A igualdade  vale para quaisquer números reais não nulos x e y.
vale para quaisquer números reais não nulos x e y. 3ª Afirmação Falsa.IV - Se x é um número real tal que
3ª Afirmação Falsa.IV - Se x é um número real tal que 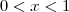 então
então 
Se 0 < x < 1 , logo
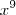
é < que
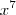
Logo,
4ª Afirmação FalsaResposta Certa Letra A: Apenas uma afirmação é verdadeira.
Eu não sei se eu acertei no cálculo e também não possuo o gabarito da questão, espero que possam me ajudar.
Desde já Agradeço!

-----------
Obs.: Primeira Postagem no Fórum!

"Quem estuda sabe mais" - Filosofia de vida!
-
sony01
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Mar 04, 2012 16:28
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Inglês
- Andamento: cursando
 por fraol » Seg Mar 05, 2012 22:32
por fraol » Seg Mar 05, 2012 22:32
Para a letra a) pense, por exemplo em x = 1 e y = 2. O seu desenvolvimento não está correto. Pense, primeiramente em elevar ao quadrado ambos os membros da expressão original e tente desenvolver a partir disso.
A letra b) é uma afirmação válida. Você quer tentar fatorar novamente?
A sua conclusão para a letra c) está correta mas, há um erro de passagem que você acabou corrigindo na sequência.
A letra d) está correta.
Se não conseguir algum desenvolvimento manda a dúvida pra cá.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Números Reais - Simplificar números reais
por ZANGARO » Ter Nov 15, 2011 18:46
- 0 Respostas
- 1945 Exibições
- Última mensagem por ZANGARO

Ter Nov 15, 2011 18:46
Álgebra Elementar
-
- [hipótese da indução] Indução matemática
por leonardoandra » Sáb Out 12, 2013 22:58
- 1 Respostas
- 2681 Exibições
- Última mensagem por leonardoandra

Seg Out 14, 2013 20:10
Equações
-
- Números reais
por citadp » Dom Jun 24, 2012 16:02
- 1 Respostas
- 1761 Exibições
- Última mensagem por e8group

Dom Jun 24, 2012 19:22
Cálculo: Limites, Derivadas e Integrais
-
- Numeros reais
por vihalmeida » Qui Nov 15, 2012 15:19
- 1 Respostas
- 2197 Exibições
- Última mensagem por DanielFerreira

Qui Nov 15, 2012 18:40
Álgebra Elementar
-
- Estimativa de numeros reais
 por Roni Martins » Qui Fev 25, 2010 15:51
por Roni Martins » Qui Fev 25, 2010 15:51
- 1 Respostas
- 2335 Exibições
- Última mensagem por Molina

Qui Fev 25, 2010 18:30
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
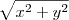 =
=  .
. .
. vale para quaisquer números reais não nulos x e y.
vale para quaisquer números reais não nulos x e y.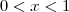 então
então 
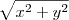 =
=  .
.![\displaystyle \sqrt[2]{x^2+y^2} = \sqrt[\not 2]{x^{ \not 2}} + \sqrt[ \not 2]{y^{ \not 2}} = x + y \displaystyle \sqrt[2]{x^2+y^2} = \sqrt[\not 2]{x^{ \not 2}} + \sqrt[ \not 2]{y^{ \not 2}} = x + y](/latexrender/pictures/b72c6a7039de78fa463d388da31963a1.png)
 .
.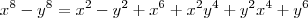
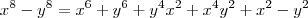

 vale para quaisquer números reais não nulos x e y.
vale para quaisquer números reais não nulos x e y.
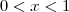 então
então 
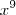 é < que
é < que