Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por joaofonseca » Sáb Mar 03, 2012 20:31
por joaofonseca » Sáb Mar 03, 2012 20:31
Num saco existem 15 bolas.Cinco verdes, cinco amarelas e cinco brancas.As bolas da mesma cor estão numeradas de 1 a 5.
Agora suponha que no saco estão algumas das 15 bolas.Nestas novas condições, uma bola é retirada do saco.Sabemos que:
-a probabilidade de a bola retirada ser amarela é 50%
-a probabilidade de a bola retirada ter o número 1 é 25%
-a probabilidade de a bola retirada ser amarela ou ter o numero 1 é 62,5%
Prove que a bola amarela com o numero 1 está no saco.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Sáb Mar 03, 2012 22:31
por LuizAquino » Sáb Mar 03, 2012 22:31
joaofonseca escreveu:Num saco existem 15 bolas.Cinco verdes, cinco amarelas e cinco brancas.As bolas da mesma cor estão numeradas de 1 a 5.
Agora suponha que no saco estão algumas das 15 bolas.Nestas novas condições, uma bola é retirada do saco.Sabemos que:
-a probabilidade de a bola retirada ser amarela é 50%
-a probabilidade de a bola retirada ter o número 1 é 25%
-a probabilidade de a bola retirada ser amarela ou ter o numero 1 é 62,5%
Prove que a bola amarela com o numero 1 está no saco.
Sejam os seguintes eventos:
A -- a bola é amarela;
N -- a bola tem número 1.
Dos conhecimentos sobre probabilidade, sabemos que:

Substituindo os dados do exercício, temos que:

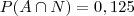
Ou seja, a probabilidade da bola retirada ser amarela e ter o número 1 é igual a 12,5%. Como essa probabilidade é diferente de 0, temos que a bola amarela com o número 1 está no saco.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fraol » Sáb Mar 03, 2012 23:10
por fraol » Sáb Mar 03, 2012 23:10
De fato, como o professor demonstrou,
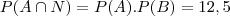
que é diferente de 0.
Com isso a probabilidade de que uma bola retirada seja Amarela e tenha o número 1 é de 12,5%.
Por outro lado se tivermos, por exemplo oito bolas no saco, quatro serão amarelas (50%) , digamos que numeradas de 2 a 5, e duas terão o número 1 (25%), digamos que seja uma verde e outra branca.
Eu havia pensado um pouco nesse problema e acho não há como provar propriamente o que foi pedido.
O que vocês acham?
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por LuizAquino » Sáb Mar 03, 2012 23:40
por LuizAquino » Sáb Mar 03, 2012 23:40
fraol escreveu:De fato, como o professor demonstrou,
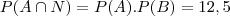
que é diferente de 0.
Com isso a probabilidade de que uma bola retirada seja Amarela e tenha o número 1 é de 12,5%.
Por outro lado se tivermos, por exemplo oito bolas no saco, quatro serão amarelas (50%) , digamos que numeradas de 2 a 5, e duas terão o número 1 (25%), digamos que seja uma verde e outra branca.
Eu havia pensado um pouco nesse problema e acho não há como provar propriamente o que foi pedido.
O que vocês acham?
O seu raciocínio tem um furo. Qual é a probabilidade da bola retirada ser amarela ou ter o número 1?
Você tem que armar um exemplo na qual essa probabilidade seja 62,5% (como informa no exercício), mas sem que haja a bola amarela de número 1.
No exemplo que você deu, temos que:
-- 4 bolas amarelas: com números de 2 até 5;
-- 1 bola verde: com o número 1;
-- 1 bola branca: com o número 1;
Você ainda precisa completar esse exemplo informando mais 2 bolas (já que o seu total era de 8). Agora tente completar de modo que aquela última probabilidade seja 62,5%, mas sem que haja a bola amarela de número 1.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fraol » Sáb Mar 03, 2012 23:56
por fraol » Sáb Mar 03, 2012 23:56
Tem razão, como sempre aliás.
Nesse caso 12,5%,

, do saco de oito bolas deveria ser de bolas amarelas e com o número 1. Ou seja uma bola. Então está provado.
Grato.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Guill » Sáb Mar 17, 2012 14:00
por Guill » Sáb Mar 17, 2012 14:00
Podemos tirar as seguintes informações:
* Temos 3 bolas com o número 1 escrito.
* Como a probabilidade de retirar uma bola amarela do saco é 50%, metade das bolas desse saco devem ser amarelas e portanto, não temos mais que 10 bolas no saco.
* Como a probabilidade de retirar uma bola com número 1 do saco é 25%, existem bolas com número 1 dentro do saco.
Agora, observe que a probabilidade de retirar uma bola amarela ou com número 1 do saco é 62,5% = 50% + 12,5%. Mas o correto seria que 75% fosse a probabilidade, o que não ocorre porque o número é menor. Isso quer dizer que existe um encontro, ou seja, existe uma bola que possui as duas características ao mesmo tempo, fazendo com que o número de amostras diminua.
Isso prova.
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Desafios Médios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Bola de beisebol
por Cleyson007 » Qua Nov 07, 2012 16:55
- 7 Respostas
- 8795 Exibições
- Última mensagem por MarceloFantini

Qui Nov 08, 2012 17:00
Física
-
- Lançamento de uma bola
por Cleyson007 » Sex Nov 09, 2012 20:25
- 2 Respostas
- 1842 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 22:44
Física
-
- Queda de uma bola em Progressão
por Carolziiinhaaah » Qua Jun 16, 2010 12:02
- 1 Respostas
- 1698 Exibições
- Última mensagem por Elcioschin

Qua Jun 16, 2010 13:38
Progressões
-
- [Limites] em uma bola aberta
por Marcos07 » Seg Jun 30, 2014 01:34
- 1 Respostas
- 1602 Exibições
- Última mensagem por e8group

Seg Jun 30, 2014 02:36
Cálculo: Limites, Derivadas e Integrais
-
- Será que esta relação geométrica esta errada?
 por Guga1981 » Qua Ago 29, 2018 18:51
por Guga1981 » Qua Ago 29, 2018 18:51
- 5 Respostas
- 17609 Exibições
- Última mensagem por Gebe

Sáb Set 01, 2018 22:27
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




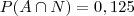

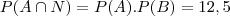 que é diferente de 0.
que é diferente de 0. , do saco de oito bolas deveria ser de bolas amarelas e com o número 1. Ou seja uma bola. Então está provado.
, do saco de oito bolas deveria ser de bolas amarelas e com o número 1. Ou seja uma bola. Então está provado.




