Boa noite,
Ananda!
Exercício típico do ITA. Com um enunciado simples, cobra vários conceitos.
Fiz no papel, mas como você ainda está tentando, vou fazer alguns comentários.
As relações que você encontrou estão certas, mas o que falta é expressar a geratriz em função de algum ângulo e do raio.
Há várias formas de se chegar ao resultado.
Considere este triângulo:

- cone.jpg (9.47 KiB) Exibido 10394 vezes
Como
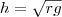
, repare que

é a tangente de

, a razão entre a altura e o raio da base, conforme diz o enunciado.
Então, uma forma de continuar seria pensar neste sub-problema: encontrar o ângulo

.
Eu tentei por este caminho, mas constatei que devemos já buscar a

, pois podemos encontrar

e

.
Como

, então, o problema estará resolvido.
As dicas para você continuar são as seguintes:
Utilize a
Lei dos Senos para expressar

em função de

e de

.
Em seguida, após substituir em uma das expressões da geratriz, por exemplo, esta:
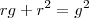
, poderá cancelar o raio e fazer uma substituição de variáveis para ter uma equação do segundo grau.
Justifique a eliminação de uma das soluções da equação do segundo grau, dependendo da escolha que fez anteriormente, por seno ou cosseno.
Depois, através da
relação fundamental da trigometria, se escolheu seno, deverá encontrar o cosseno, ou vice-versa.
Por fim, calcule a tangente.
Você também pode substituir

na expressão de

que escreveu.
Ananda, depois comente o seu progresso ou alguma nova dúvida, para que eu possa enfatizar algum detalhe ao postar uma resolução completa.
Até mais.
![\sqrt[]{\frac{\sqrt[]{5}+1}{2}} \sqrt[]{\frac{\sqrt[]{5}+1}{2}}](/latexrender/pictures/3e28ecbdbdb960d05ad0c1d8e6c37a64.png)
![h=\sqrt[]{r.g} h=\sqrt[]{r.g}](/latexrender/pictures/dff392f022f156b8ea9ee353742c3882.png) (média geométrica)
(média geométrica)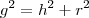
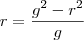
![\frac{h}{r}= \frac{\sqrt[]{g^2-r^2}}{\frac{g^2-r^2}{g}} \frac{h}{r}= \frac{\sqrt[]{g^2-r^2}}{\frac{g^2-r^2}{g}}](/latexrender/pictures/babb4fcc0cfd612e2357db0ae6c6e036.png) (Provavelmente há um modo de "cortar", mas meu cérebro não me ajudou ainda).
(Provavelmente há um modo de "cortar", mas meu cérebro não me ajudou ainda).
 (Aqui achei que dará mais trabalho do que o anterior, já que tem raiz quarta).
(Aqui achei que dará mais trabalho do que o anterior, já que tem raiz quarta).

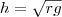 , repare que
, repare que  é a tangente de
é a tangente de  , a razão entre a altura e o raio da base, conforme diz o enunciado.
, a razão entre a altura e o raio da base, conforme diz o enunciado. , pois podemos encontrar
, pois podemos encontrar  e
e  .
. , então, o problema estará resolvido.
, então, o problema estará resolvido. em função de
em função de  e de
e de 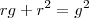 , poderá cancelar o raio e fazer uma substituição de variáveis para ter uma equação do segundo grau.
, poderá cancelar o raio e fazer uma substituição de variáveis para ter uma equação do segundo grau.

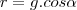
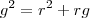
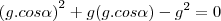
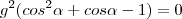
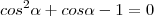
![cos\alpha=\frac{-1\pm\sqrt[]{5}}{2} cos\alpha=\frac{-1\pm\sqrt[]{5}}{2}](/latexrender/pictures/4daaed7491d8d9edfd348b4b8a7e608e.png)
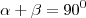
![\frac{-1+\sqrt[]{5}}{2} \frac{-1+\sqrt[]{5}}{2}](/latexrender/pictures/386f35e12d26c1ca010e15050369fce4.png)
![sen\alpha=\sqrt[]{1-{\left(\frac{\sqrt[]{5}-1}{2} \right)}^{2}} sen\alpha=\sqrt[]{1-{\left(\frac{\sqrt[]{5}-1}{2} \right)}^{2}}](/latexrender/pictures/c38b4cbbdfb5f0d5d04d642b443c4b31.png)
![sen\alpha=\sqrt[]{\frac{\sqrt[]{5}-1}{2}} sen\alpha=\sqrt[]{\frac{\sqrt[]{5}-1}{2}}](/latexrender/pictures/754c41086681e9354aef3b50d848947a.png)
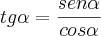
![{tg}^{2}\alpha=\frac{2}{\sqrt[]{5}-1} {tg}^{2}\alpha=\frac{2}{\sqrt[]{5}-1}](/latexrender/pictures/4dbff52ca282926a6b8c93a540f1e315.png)
![tg\alpha=\sqrt[]{\frac{2}{\sqrt[]{5}-1}} tg\alpha=\sqrt[]{\frac{2}{\sqrt[]{5}-1}}](/latexrender/pictures/c58b92c28109f8c7c9cf1bba74a5cad8.png)
![tg\alpha=\frac{h}{r}=\sqrt[]{\frac{\sqrt[]{5}+1}{2}} tg\alpha=\frac{h}{r}=\sqrt[]{\frac{\sqrt[]{5}+1}{2}}](/latexrender/pictures/043b5a4a655c7b5724d43bfe8a8b2b2e.png)
 .
. .
. .
.