 por jmontenegro » Ter Fev 28, 2012 14:56
por jmontenegro » Ter Fev 28, 2012 14:56
Gente,
Desculpa eu nem tentar mas eu realmente nao sei nem de onde tirar essa informacao.
Meus livros (os que tenho em casa) nao tem esse tipo de exercicio que associe uma elipse a uma equacao geral de reta...
Se alguem puder me dar qualquer tipo de orientacao, ja esta valendo!

Abraco,
Julia
-
jmontenegro
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Fev 19, 2012 11:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ADM
- Andamento: formado
 por LuizAquino » Ter Fev 28, 2012 15:37
por LuizAquino » Ter Fev 28, 2012 15:37
Prezado
jmontenegro,
Para manter o fórum organizado, nós solicitamos que o texto do exercício seja todo digitado no tópico.
Além disso, ao enviar um texto na forma de imagem você prejudica o sistema de busca do fórum.
Por favor, digite o texto completo do exercício.
Apenas envie como uma imagem o que for estritamente necessário.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jmontenegro » Ter Fev 28, 2012 21:46
por jmontenegro » Ter Fev 28, 2012 21:46
Luiz Aquino, perdão!!! Eu não sabia como proceder com problemas que envolvem uma imagem.
Agradeço a sua atenção.
Agora vai digitado...
Os pontos A(2,1) e B(0,3) pertencem à elipse E. A elipse E’foi obtida por uma homotetia de centro na origem do sistema de coordenadas.
(a imagem referente ao problema está em
http://imageshack.us/photo/my-images/802/problemaq.jpg)
Os pontos A’ e B’ são, respectivamente, as imagens de A e B por essa homotetia. O ponto B’ pertence ao eixo das ordenadas e tem abscissa igual a 1.
O ponto A’ pertence à reta s, perpendicular a reta AA’. A equação geral da reta s é:
(A) 12x + 6y ? 5 = 0
(B) 12x + 6y + 3 = 0
(C) 6x + 3y + 5 = 0
(D) 6x + 3y ?1 = 0
(E) 6x + 3y ? 5 = 0
-
jmontenegro
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Fev 19, 2012 11:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ADM
- Andamento: formado
 por LuizAquino » Qua Fev 29, 2012 02:23
por LuizAquino » Qua Fev 29, 2012 02:23
jmontenegro escreveu:Os pontos A(2,1) e B(0,3) pertencem à elipse E. A elipse E’foi obtida por uma homotetia de centro na origem do sistema de coordenadas.
(a imagem referente ao problema está em
http://imageshack.us/photo/my-images/802/problemaq.jpg)
Os pontos A’ e B’ são, respectivamente, as imagens de A e B por essa homotetia. O ponto B’ pertence ao eixo das ordenadas e tem abscissa igual a 1.
O ponto A’ pertence à reta s, perpendicular a reta AA’. A equação geral da reta s é:
(A) 12x + 6y ? 5 = 0
(B) 12x + 6y + 3 = 0
(C) 6x + 3y + 5 = 0
(D) 6x + 3y ?1 = 0
(E) 6x + 3y ? 5 = 0
Uma homotetia é caracterizada por seu centro O e por sua constante de proporção k.
Devido a homotetia, devemos ter:


Dos dados do exercício, temos que:
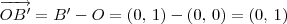

Comparando esses dois vetores, temos que:
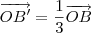
Ou seja, a constante de proporção da homotetia é k=1/3.
Sabendo dessa informação, você pode descobrir quais são as coordenadas do ponto A’.
Em seguida, você pode determinar o coeficiente angular da reta que passa por AA’. Vamos supor que ele seja
m.
Por fim, você pode determinar a reta perpendicular a AA’ e que passa por A’. Lembre-se que o coeficiente angular dessa reta será -1/
m.
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- equação de uma elipse
por max » Dom Mar 20, 2011 18:44
- 2 Respostas
- 1893 Exibições
- Última mensagem por max

Dom Mar 20, 2011 22:01
Geometria Analítica
-
- equação da elipse
por Andreza » Qui Jan 26, 2012 11:59
- 3 Respostas
- 2703 Exibições
- Última mensagem por LuizAquino

Qui Jan 26, 2012 14:01
Geometria Analítica
-
- Equação da elipse
por marinalcd » Qui Ago 23, 2012 19:14
- 1 Respostas
- 1279 Exibições
- Última mensagem por MarceloFantini

Qui Ago 23, 2012 20:29
Geometria Analítica
-
- Equação da elipse
por marcos machado » Sáb Mai 31, 2014 13:57
- 1 Respostas
- 1269 Exibições
- Última mensagem por DanielFerreira

Sáb Jul 05, 2014 16:21
Geometria Analítica
-
- Ajuda para resolver equação para calcular velocidade média
por marcorrer » Sex Fev 24, 2012 13:10
- 0 Respostas
- 3703 Exibições
- Última mensagem por marcorrer

Sex Fev 24, 2012 13:10
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.