 por alfabeta » Ter Fev 28, 2012 11:53
por alfabeta » Ter Fev 28, 2012 11:53
(Ufmg 2002) Na figura abaixo, a circunferência tem centro O e o seu raio tem a mesma medida do segmento BC. Sejam alfa a medida do ângulo AÔD e ’beta a medida do ângulo alfa e beta
nao consigo copiar e colar a figura...por favor me ajude.
-
alfabeta
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Ter Fev 28, 2012 11:37
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Ter Fev 28, 2012 16:05
por MarceloFantini » Ter Fev 28, 2012 16:05
Alfabeta, embaixo da caixa de digitação procure uma pequena aba azul que diz "Adicionar um anexo". Você poderá anexar a figura e assim veremos o que o enunciado que dizer. Não se esqueça de completá-lo, pois ainda faltam dados e a pergunta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por alfabeta » Ter Fev 28, 2012 20:36
por alfabeta » Ter Fev 28, 2012 20:36
Obrigado pela ajuda!
Segue a questão:
(Ufmg) Na figura abaixo, a circunferência tem centro O e o seu raio tem a mesma medida do segmento BC. Sejam ? a medida do ângulo AÔD e ? a medida do ângulo ACD.
Ache ? em função de ?
a) ? = 5?/2 b) ? = 3 ? c) ? = 7 ? /2 d) ? = 2 ? e) ?= ?
Tentativa de resolução: primeiro, eu disse que o arco AD é igual a ?, que é o angulo central. ? é o angulo externo do triangulo AOB, portanto vale B mais OÂC. não sei como achar este último angulo.
-
alfabeta
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Ter Fev 28, 2012 11:37
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Qua Fev 29, 2012 13:12
por LuizAquino » Qua Fev 29, 2012 13:12
alfabeta escreveu:(Ufmg) Na figura abaixo, a circunferência tem centro O e o seu raio tem a mesma medida do segmento BC. Sejam ? a medida do ângulo AÔD e ? a medida do ângulo ACD.
Ache ? em função de ?
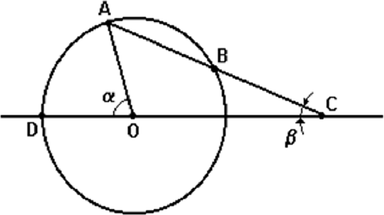
- figura.png (9.44 KiB) Exibido 12647 vezes
alfabeta escreveu:Tentativa de resolução: primeiro, eu disse que o arco AD é igual a ?, que é o angulo central. ? é o angulo externo do triangulo AOB, portanto vale B mais OÂC. não sei como achar este último angulo.
Observe a figura abaixo.
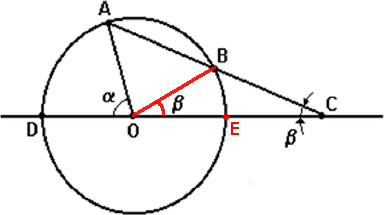
- figura2.png (28.13 KiB) Exibido 12647 vezes
Foi informado que BC mede o mesmo que o raio. Isso significa que BC = OB. Sendo assim, o triângulo OBC é isósceles. Podemos então dizer que
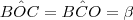
.
Além disso, o triângulo AOB também é isósceles, pois OA e OB são raios da circunferência. Podemos então dizer que

.
Note que o ângulo
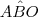
é externo ao triângulo OBC. Sendo assim, temos que
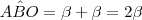
.
Temos então que
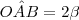
.
Agora termine o exercício.
Editado pela última vez por
LuizAquino em Qui Mar 01, 2012 02:21, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por alfabeta » Qua Fev 29, 2012 22:42
por alfabeta » Qua Fev 29, 2012 22:42
Professor Luiz Aquino, muito obrigada! Entendi!
=
Finalizando: Como alfa é ângulo externo de AOC, temos que alfa = beta + 2 beta = 3 beta!
-
alfabeta
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Ter Fev 28, 2012 11:37
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Angulos na Circunferencia
por vyhonda » Seg Mar 29, 2010 11:12
- 2 Respostas
- 12467 Exibições
- Última mensagem por vyhonda

Qua Mar 31, 2010 13:18
Geometria Plana
-
- Ângulos na Circunferência
por Douglaspimentel » Qua Set 15, 2010 00:17
- 1 Respostas
- 4991 Exibições
- Última mensagem por gichan

Qua Set 15, 2010 02:33
Geometria Plana
-
- [Ângulos numa Circunferência] (UNIFOR-CE/1998)
 por eiji » Sex Abr 13, 2012 20:57
por eiji » Sex Abr 13, 2012 20:57
- 2 Respostas
- 9915 Exibições
- Última mensagem por eiji

Sex Abr 13, 2012 21:28
Geometria Plana
-
- [circunferência] Questão de reta secante a circunferência
por danielleecb » Qui Jun 07, 2012 23:26
- 1 Respostas
- 1876 Exibições
- Última mensagem por MarceloFantini

Sex Jun 08, 2012 12:24
Geometria Analítica
-
- Ângulos
 por admin » Sex Set 07, 2007 06:42
por admin » Sex Set 07, 2007 06:42
- 3 Respostas
- 13553 Exibições
- Última mensagem por Numwantida

Qui Mai 24, 2018 05:06
Pérolas
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






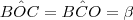 .
. .
.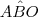 é externo ao triângulo OBC. Sendo assim, temos que
é externo ao triângulo OBC. Sendo assim, temos que 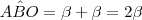 .
.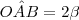 .
.






