 por watson » Qua Fev 22, 2012 16:33
por watson » Qua Fev 22, 2012 16:33
Pessoal Boa tarde !
Por favor alguem pode me ajudar ,como faço essa conta .
Determine a inversa das matrizes .
2x2.
| 2 4 |
| |
|1 5 |
2 4
1 5
Desde já muito segue o meu e-mail
wateson@ig.com.br
-
watson
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Fev 22, 2012 16:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Andreza » Qua Fev 22, 2012 17:30
por Andreza » Qua Fev 22, 2012 17:30
Vc multiplica a matriz por
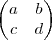
que é igual a matriz identidade

Monta o sistema e resolve as equações.
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
 por watson » Qua Fev 22, 2012 19:14
por watson » Qua Fev 22, 2012 19:14
Andreza Boa tarde !
Até ai eu sei fazer ,eu identifiquei que o valor dessa determinante é diferente de 0 .
10-4 =6 ,depois multipliquei pelas incognita x,y,z,t .Ai a minha dúvida entra agora ,eu não sei fazer o metodo da adição e substituição.
2.x+4.z <---- nesse ponto eu nao sei como exercer o metodo da adição e substituição
1.x+5.z
Desde muito Obrigado pelo retorno,me desculpe por alguma coisa ...
Aguardo retorno
God Bless You !
-
watson
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Fev 22, 2012 16:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por MarceloFantini » Qua Fev 22, 2012 22:07
por MarceloFantini » Qua Fev 22, 2012 22:07
A definição de matriz inversa é: dada uma matriz

, diremos que

é sua inversa se e somente se

onde

é a identidade. Uma condição necessária e suficiente para que uma matriz seja invertível é que seu determinante seja
diferente de zero. Como você já verificou, isto é verdade e portanto podemos encontrar a matriz B.
Usando isto, seja
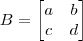
. Faça

e iguale a
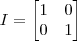
. Você terá um sistema de quatro equações e quatro incógnitas, basta resolver.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Qua Fev 22, 2012 22:44
por LuizAquino » Qua Fev 22, 2012 22:44
watson escreveu:Ai a minha dúvida entra agora ,eu não sei fazer o metodo da adição e substituição.
2.x+4.z <---- nesse ponto eu nao sei como exercer o metodo da adição e substituição
1.x+5.z
Eu recomendo que você assista as videoaulas "Matemática - Aula 21 - Matriz Inversa", "Matemática - Aula 22 - Introdução aos Sistemas Lineares" e "Matemática - Aula 23 - Sistemas Lineares". Essas aulas estão disponíveis no canal do Nerckie:
http://www.youtube.com/nerckie
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5153 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
-
- [Sistemas lineares] - Método por adição
por Pstefani » Dom Set 04, 2011 23:52
- 6 Respostas
- 4203 Exibições
- Última mensagem por Pstefani

Ter Set 06, 2011 09:47
Sistemas de Equações
-
- Matrizes - [Método de gauss]
por beerzy » Ter Set 22, 2015 20:42
- 0 Respostas
- 4478 Exibições
- Última mensagem por beerzy

Ter Set 22, 2015 20:42
Matrizes e Determinantes
-
- [funções inversas]
por Ana_Rodrigues » Ter Jan 24, 2012 17:46
- 2 Respostas
- 1731 Exibições
- Última mensagem por Ana_Rodrigues

Ter Jan 24, 2012 22:33
Funções
-
- funções inversas
por Edgard Guarido » Sex Mar 07, 2014 18:53
- 2 Respostas
- 2597 Exibições
- Última mensagem por Edgard Guarido

Qui Mar 13, 2014 15:54
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



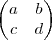 que é igual a matriz identidade
que é igual a matriz identidade 


 , diremos que
, diremos que  é sua inversa se e somente se
é sua inversa se e somente se  onde
onde  é a identidade. Uma condição necessária e suficiente para que uma matriz seja invertível é que seu determinante seja diferente de zero. Como você já verificou, isto é verdade e portanto podemos encontrar a matriz B.
é a identidade. Uma condição necessária e suficiente para que uma matriz seja invertível é que seu determinante seja diferente de zero. Como você já verificou, isto é verdade e portanto podemos encontrar a matriz B.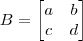 . Faça
. Faça  e iguale a
e iguale a 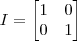 . Você terá um sistema de quatro equações e quatro incógnitas, basta resolver.
. Você terá um sistema de quatro equações e quatro incógnitas, basta resolver.


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
