1) COM OS ALGARISMOS 1,2,3,4 E 5 E SEM REPETIÇÃO PODE SE ESCREVER X NUMEROS MAIORES QUE 2500. O VALOR DE X É ?
Tentei assim na 1 opção sao 4 numeros maiores que que 2, na 2 opção 1, na 3 opção 5 e na 4 opção 4, então: 4x1x5x4=80, mas a resposta é 198. Me ajude



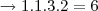 ou
ou 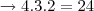 ou
ou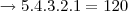
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)