Andrewo escreveu:1-(VUNESP)Duas empreiteiras farão simultaneamente a pavimentação de uma estrada, cada uma trabalhando a partir de uma das extremidades. Se uma delas pavimentar 2/5 da estrada e outra 81 km, a extensão dessa estrada é de:
Considere que x é o tamanho da estrada.
A Empresa 1 pavimentou
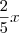
.
A Empresa 2 pavimentou 81 Km.
Se juntarmos essas duas partes, devemos ter o tamanho da estrada. Sendo assim, podemos montar a equação:
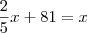
Agora tente terminar o exercício.
Andrewo escreveu:2-(METODISTA)Um elevador pode levar 20 adultos ou 24 crianças.Se 15 adultos já estão no elevador, quantas crianças podem ainda entrar?
Sejam a e c quantidade de adultos e crianças, respectivamente.
A capacidade máxima do elevador é 20a ou 24c. Ou seja, 20a ou 24c representam um mesmo peso.
Sendo assim, podemos dizer que 20a = 24c. Ou ainda, podemos dizer que o peso de cada adulto corresponde a
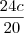
do peso de cada criança.
Agora pense no seguinte: Se o peso de 1 adulto corresponde a
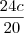
do peso de 1 criança, então o peso de 15 adultos corresponde ao peso de quantas crianças?
Tente terminar o exercício.
Andrewo escreveu:3-(FUVEST)-Duas garotas realizam um serviço de datilografia. A mais experiente consegue faze-lo em duas horas, a outra em 3 horas.Se dividirmos o serviço de modo que as duas juntas possam fazer no menor tempo possível esse tempo será:
Suponha que a garota 1 é a mais experiente. Se ela faz o trabalho T em 2 horas, então a cada hora ela faz
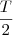
do trabalho.
Quanto a garota 2, se ela faz o trabalho T em 3 horas, então a cada hora ela faz
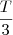
do trabalho.
Se as garotas trabalharem juntas, então a cada hora elas farão

do trabalho.
Agora pense no seguinte: se em 1 hora (ou 60 minutos) elas fazem
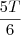
do trabalho, então em quantas horas (ou minutos) elas fariam o trabalho todo (isto é, T)?
Tente terminar o exercício.
Andrewo escreveu:(...) me dessem dicas (se existem) pra eu melhorar minha interpretação e ajudar na hora de resolver outros problemas.
Leia mais! A interpretação de texto é fundamental não só na Matemática como em qualquer outra disciplina.
Além disso, procure dividir o enunciado do exercício em diversas partes. Você deve entender cada uma dessas partes. Se uma delas ficar sem entendimento, então é provável que você não consiga concluir o exercício. E por fim, sempre verifique a sua resposta. Confira se ela condiz com os dados do exercício.




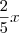 .
.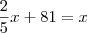
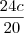 do peso de cada criança.
do peso de cada criança.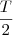 do trabalho.
do trabalho.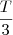 do trabalho.
do trabalho. do trabalho.
do trabalho.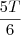 do trabalho, então em quantas horas (ou minutos) elas fariam o trabalho todo (isto é, T)?
do trabalho, então em quantas horas (ou minutos) elas fariam o trabalho todo (isto é, T)?
 =
=  ou seja: cada adulto equivale a
ou seja: cada adulto equivale a 



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)