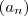 tal que
tal que 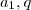 e
e  são números reais dados, com q diferente de 1 , e, para todo n inteiro, n > 0, tem-se que:
são números reais dados, com q diferente de 1 , e, para todo n inteiro, n > 0, tem-se que:
(A) Mostre por indução que
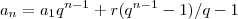
Eu ja provei a igualdade verdadeira para n=1:
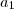 =
= 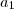


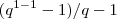
=>
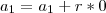 =>
=>  verdade.
verdade.Suponhamos esta igualdade verdade para algum n. Para n + 1:
 . Tentei resolver porém não consigo fazer a prova utilizando recorrência. Alguém pode me ajudar?
. Tentei resolver porém não consigo fazer a prova utilizando recorrência. Alguém pode me ajudar?

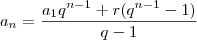
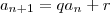 ,
,

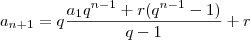
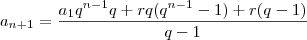 .
. divide apenas o
divide apenas o 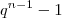 , que está após o r
, que está após o r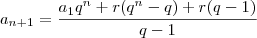 .
.  .
. .
.  em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.