 por kalschne » Qui Fev 16, 2012 20:51
por kalschne » Qui Fev 16, 2012 20:51
Estou quebrando a cabeça em um exercício que meu professor de Cálculo vetorial passou na sala, to precisando de ajuda:
Suponha que uma circunferência tenha raio "a" e o eixo x seja a reta fixa sobre a qual essa circunferência gira. Considere o ponto p na origem quando o centro da circunferência está em (0,a). Determine as equações paramétricas da curva C descrito por este ponto p quando a circunferência gira sobre o eixo.
Eu consigo imaginar o gráfico, mas não estou conseguindo achar as equações paramétricas dessa curva. Alguém me da uma ajuda ai =D
-
kalschne
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Fev 16, 2012 20:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por MarceloFantini » Qui Fev 16, 2012 22:18
por MarceloFantini » Qui Fev 16, 2012 22:18
Eu consegui parametrizar para uma volta completa, note que a curva descrita será uma circunferência com centro em
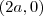
e raio

, daí
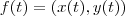
onde
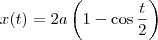
e
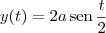
para
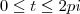
.
Cada volta completa será dessa forma, mas não sei condensar (se é possível) qualquer volta em uma única equação.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por kalschne » Qui Fev 16, 2012 22:48
por kalschne » Qui Fev 16, 2012 22:48
Valeu, consegui entender =)
-
kalschne
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Fev 16, 2012 20:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações Paramétricas] Comprimento da Curva
por vmouc » Ter Mar 27, 2012 14:53
- 3 Respostas
- 2356 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 15:10
Cálculo: Limites, Derivadas e Integrais
-
- [Equações Paramétricas - Derivada da Curva]
por raimundoocjr » Sáb Out 19, 2013 20:38
- 0 Respostas
- 796 Exibições
- Última mensagem por raimundoocjr

Sáb Out 19, 2013 20:38
Cálculo: Limites, Derivadas e Integrais
-
- Equações cartesianas e equações paramétricas
por Victor Mello » Sáb Ago 23, 2014 16:24
- 1 Respostas
- 3426 Exibições
- Última mensagem por Russman

Sáb Ago 23, 2014 18:29
Funções
-
- Equaçoes parametricas
por angels900 » Ter Jan 31, 2012 14:35
- 6 Respostas
- 3721 Exibições
- Última mensagem por LuizAquino

Ter Jan 31, 2012 17:04
Geometria Analítica
-
- [Equações Paramétricas - Espaço]
por raimundoocjr » Ter Set 24, 2013 20:40
- 2 Respostas
- 1860 Exibições
- Última mensagem por raimundoocjr

Qua Set 25, 2013 19:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



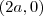 e raio
e raio  , daí
, daí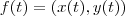 onde
onde 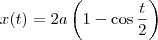 e
e 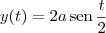 para
para 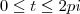 .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.