1 - Ache a derivada em relação a x para a função

2 - Ache a área da região limitada pela curva dada: y = x³ - x e y = 0 (eixo x).
Já tentei encontrar a solução na internet, em 5 livros e uma apostila, mas os exemplos e textos não são muito claros.
Peço a gentileza se alguém pode me ajudar, desde já agradeço.


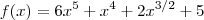
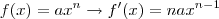
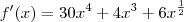
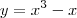 e
e  (eixo x).
(eixo x).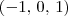 o que significa que ela intercepta o eixo x nesses tres pontos.
o que significa que ela intercepta o eixo x nesses tres pontos.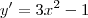 os pontos em que a derivada se anula são os máximos e mínimos da função e temos para
os pontos em que a derivada se anula são os máximos e mínimos da função e temos para 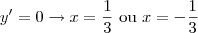 . Temos um máximo em
. Temos um máximo em 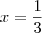 e um mínimo em
e um mínimo em  . Com esses elementos podemos esboçar o gráfico
. Com esses elementos podemos esboçar o gráfico
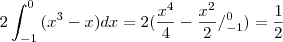

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)