 por Andrewo » Seg Fev 13, 2012 16:58
por Andrewo » Seg Fev 13, 2012 16:58
Eaí pessoal, to com umas dúvidas numas continhas de vestiba( está quase acabando a parte de radicais, paciência please

)
![\sqrt[3]{\frac{a}{b}\sqrt[]{\frac{a}{b}}} \sqrt[3]{\frac{a}{b}\sqrt[]{\frac{a}{b}}}](/latexrender/pictures/23a4ae54d10ad257dbb343d12ef15367.png)
Resposta :
![\sqrt[]{\frac{a}{b}} \sqrt[]{\frac{a}{b}}](/latexrender/pictures/42e6680459316c84bb1fb8314be42226.png)
O que eu tentei fazer :
![\sqrt[3]{\frac{a}{b}.{\frac{a}{b}}^{\frac{1}{2}}} \sqrt[3]{\frac{a}{b}.{\frac{a}{b}}^{\frac{1}{2}}}](/latexrender/pictures/4c0a68a36d6923ca02ffcc9e2a7dbc9d.png)
=
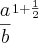
=
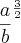
=
![\sqrt[3]{\sqrt[]{{\frac{a}{b}}^{3}}} \sqrt[3]{\sqrt[]{{\frac{a}{b}}^{3}}}](/latexrender/pictures/259287c25e3eb8fcda18c5eb3c45dc33.png)
=
![\sqrt[6]{{\frac{a}{b}}^{3}}} \sqrt[6]{{\frac{a}{b}}^{3}}}](/latexrender/pictures/9cc1c7f76a4271e17adb409c83c3d44d.png)
2- O número
![3+2\sqrt[]{2} 3+2\sqrt[]{2}](/latexrender/pictures/8a4f488b4902771b4ebfb90b4b32531b.png)
é igual a raíz quadrada de:
Aí entre as opções dadas a resposta certa é
![17+12\sqrt[]{2} 17+12\sqrt[]{2}](/latexrender/pictures/814ff90ef7adadf59742a2e08edbae67.png)
Nessa eu tentei desenvolver a partir da resposta pra chegar na conta que tá no enunciado
![\sqrt[]{17+12\sqrt[]{2}} \sqrt[]{17+12\sqrt[]{2}}](/latexrender/pictures/4a23c1c92127489738607eae78cecb15.png)
Nessa conta eu tentei jogar o 12 pra dentro da raiz e depois tentei tranformar a raiz em potência, mas não consegui desenvolver.
3-

Bom, comecei fazendo assim :
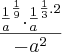
=

Tá certo? dá pra continuar daí?
Vlw pessoal



-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Seg Fev 13, 2012 18:04
por MarceloFantini » Seg Fev 13, 2012 18:04
Na primeira questão você esqueceu de somar a potência no denominador, refaça lembrando disso que seu resultado sairá correto.
Na segunda, veja que
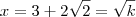
. Agora, basta elevar a o quadrado para encontrar o número k.

Espero que a fração na terceira seja esta:
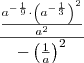
Vamos resolver por partes:
No numerador temos

.
Daí,
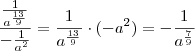
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Arkanus Darondra » Seg Fev 13, 2012 18:20
por Arkanus Darondra » Seg Fev 13, 2012 18:20
Andrewo escreveu:![\sqrt[3]{\frac{a}{b}\sqrt[]{\frac{a}{b}}} \sqrt[3]{\frac{a}{b}\sqrt[]{\frac{a}{b}}}](/latexrender/pictures/23a4ae54d10ad257dbb343d12ef15367.png)
O que eu tentei fazer :
![\sqrt[3]{\frac{a}{b}.{\frac{a}{b}}^{\frac{1}{2}}} \sqrt[3]{\frac{a}{b}.{\frac{a}{b}}^{\frac{1}{2}}}](/latexrender/pictures/4c0a68a36d6923ca02ffcc9e2a7dbc9d.png)
=
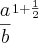
=
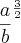
=
![\sqrt[3]{\sqrt[]{{\frac{a}{b}}^{3}}} \sqrt[3]{\sqrt[]{{\frac{a}{b}}^{3}}}](/latexrender/pictures/259287c25e3eb8fcda18c5eb3c45dc33.png)
=
![\sqrt[6]{{\frac{a}{b}}^{3}}} \sqrt[6]{{\frac{a}{b}}^{3}}}](/latexrender/pictures/9cc1c7f76a4271e17adb409c83c3d44d.png)
Cuidado! Tente fazer considerando esta passagem:
![\sqrt[3]{\frac{a}{b}\sqrt{\frac{a}{b}}} \Rightarrow \sqrt[3]{\frac{a}{b}.\frac{a^{\frac12}}{b^{\frac12}}} \sqrt[3]{\frac{a}{b}\sqrt{\frac{a}{b}}} \Rightarrow \sqrt[3]{\frac{a}{b}.\frac{a^{\frac12}}{b^{\frac12}}}](/latexrender/pictures/ea24b276823e85d84043e06a76af0e7a.png)
Andrewo escreveu:2- O número
![3+2\sqrt[]{2} 3+2\sqrt[]{2}](/latexrender/pictures/8a4f488b4902771b4ebfb90b4b32531b.png)
é igual a raíz quadrada de:
Basta fazer

Andrewo escreveu:3-

Bom, comecei fazendo assim :
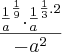
=

Tá certo? dá pra continuar daí?
Cuidado!
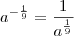
. O mesmo vale para o que está entre parênteses.
Fiz a resolução da mesma:

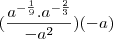
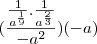
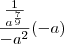

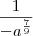
![\frac{a}{\sqrt[9]{-a^7}} \frac{a}{\sqrt[9]{-a^7}}](/latexrender/pictures/1f3b74b1d4f35bd0ac31e68e1f5a8b23.png)
Qualquer problema, retorne.
Espero que ajude.

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Andrewo » Ter Fev 14, 2012 11:10
por Andrewo » Ter Fev 14, 2012 11:10
Arkanus Darondra escreveu:Andrewo escreveu:![\sqrt[3]{\frac{a}{b}\sqrt[]{\frac{a}{b}}} \sqrt[3]{\frac{a}{b}\sqrt[]{\frac{a}{b}}}](/latexrender/pictures/23a4ae54d10ad257dbb343d12ef15367.png)
O que eu tentei fazer :
![\sqrt[3]{\frac{a}{b}.{\frac{a}{b}}^{\frac{1}{2}}} \sqrt[3]{\frac{a}{b}.{\frac{a}{b}}^{\frac{1}{2}}}](/latexrender/pictures/4c0a68a36d6923ca02ffcc9e2a7dbc9d.png)
=
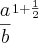
=
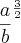
=
![\sqrt[3]{\sqrt[]{{\frac{a}{b}}^{3}}} \sqrt[3]{\sqrt[]{{\frac{a}{b}}^{3}}}](/latexrender/pictures/259287c25e3eb8fcda18c5eb3c45dc33.png)
=
![\sqrt[6]{{\frac{a}{b}}^{3}}} \sqrt[6]{{\frac{a}{b}}^{3}}}](/latexrender/pictures/9cc1c7f76a4271e17adb409c83c3d44d.png)
Cuidado! Tente fazer considerando esta passagem:
![\sqrt[3]{\frac{a}{b}\sqrt{\frac{a}{b}}} \Rightarrow \sqrt[3]{\frac{a}{b}.\frac{a^{\frac12}}{b^{\frac12}}} \sqrt[3]{\frac{a}{b}\sqrt{\frac{a}{b}}} \Rightarrow \sqrt[3]{\frac{a}{b}.\frac{a^{\frac12}}{b^{\frac12}}}](/latexrender/pictures/ea24b276823e85d84043e06a76af0e7a.png)
Mesmo eu considerando essa passagem, não bate com o resultado do gabarito pois vai ficar a mesma coisa:
![\sqrt[3]{{\frac{a}{b}}^{\frac{3}{2}}} \sqrt[3]{{\frac{a}{b}}^{\frac{3}{2}}}](/latexrender/pictures/df1b16fd03be1b446154cac49e152b65.png)
=
![\sqrt[3]{\sqrt[]{{\left( \frac{a}{b} \right)}^{3}}} \sqrt[3]{\sqrt[]{{\left( \frac{a}{b} \right)}^{3}}}](/latexrender/pictures/f02a854bd15f1d2eea4ae842d540c99c.png)
=
![\sqrt[6]{{\left( \frac{a}{b} \right)}^{3}} \sqrt[6]{{\left( \frac{a}{b} \right)}^{3}}](/latexrender/pictures/3f2aa6945c3a715f3329ce88e7bf4afb.png)
-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Arkanus Darondra » Ter Fev 14, 2012 13:01
por Arkanus Darondra » Ter Fev 14, 2012 13:01
Exato. Agora divida o índice do radical e o expoente do radicando por 3.

Obs.: Cuidado com o detalhe do expoente em sua passagem. O correto seria
![\sqrt[3]{({\frac{a}{b}})^{\frac{3}{2}}} \sqrt[3]{({\frac{a}{b}})^{\frac{3}{2}}}](/latexrender/pictures/ffd57e44d1b14cc3dc3e0219fa489f20.png)
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Radicais
por agfp5 » Sáb Out 30, 2010 08:50
- 2 Respostas
- 2330 Exibições
- Última mensagem por agfp5

Sáb Out 30, 2010 09:10
Geometria Plana
-
- Radicais
por Andrewo » Qua Fev 01, 2012 13:43
- 8 Respostas
- 4114 Exibições
- Última mensagem por LuizAquino

Qua Fev 08, 2012 12:22
Álgebra Elementar
-
- Radicais II
por Andrewo » Qui Fev 09, 2012 19:38
- 3 Respostas
- 1874 Exibições
- Última mensagem por MarceloFantini

Sex Fev 10, 2012 11:32
Álgebra Elementar
-
- Problema com radicais
por thadeu » Ter Nov 24, 2009 20:27
- 0 Respostas
- 1011 Exibições
- Última mensagem por thadeu

Ter Nov 24, 2009 20:27
Álgebra Elementar
-
- Limite com radicais
por valeuleo » Qui Mar 31, 2011 08:46
- 3 Respostas
- 5425 Exibições
- Última mensagem por LuizAquino

Qui Mar 31, 2011 11:41
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{\frac{a}{b}\sqrt[]{\frac{a}{b}}} \sqrt[3]{\frac{a}{b}\sqrt[]{\frac{a}{b}}}](/latexrender/pictures/23a4ae54d10ad257dbb343d12ef15367.png)
![\sqrt[]{\frac{a}{b}} \sqrt[]{\frac{a}{b}}](/latexrender/pictures/42e6680459316c84bb1fb8314be42226.png)
![\sqrt[3]{\frac{a}{b}.{\frac{a}{b}}^{\frac{1}{2}}} \sqrt[3]{\frac{a}{b}.{\frac{a}{b}}^{\frac{1}{2}}}](/latexrender/pictures/4c0a68a36d6923ca02ffcc9e2a7dbc9d.png) =
= 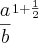 =
= 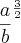
![\sqrt[3]{\sqrt[]{{\frac{a}{b}}^{3}}} \sqrt[3]{\sqrt[]{{\frac{a}{b}}^{3}}}](/latexrender/pictures/259287c25e3eb8fcda18c5eb3c45dc33.png) =
= ![\sqrt[6]{{\frac{a}{b}}^{3}}} \sqrt[6]{{\frac{a}{b}}^{3}}}](/latexrender/pictures/9cc1c7f76a4271e17adb409c83c3d44d.png)
![3+2\sqrt[]{2} 3+2\sqrt[]{2}](/latexrender/pictures/8a4f488b4902771b4ebfb90b4b32531b.png) é igual a raíz quadrada de:
é igual a raíz quadrada de:![17+12\sqrt[]{2} 17+12\sqrt[]{2}](/latexrender/pictures/814ff90ef7adadf59742a2e08edbae67.png)
![\sqrt[]{17+12\sqrt[]{2}} \sqrt[]{17+12\sqrt[]{2}}](/latexrender/pictures/4a23c1c92127489738607eae78cecb15.png)

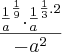






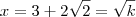 . Agora, basta elevar a o quadrado para encontrar o número k.
. Agora, basta elevar a o quadrado para encontrar o número k.
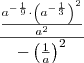
 .
.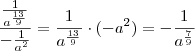 .
.

![\sqrt[3]{\frac{a}{b}\sqrt{\frac{a}{b}}} \Rightarrow \sqrt[3]{\frac{a}{b}.\frac{a^{\frac12}}{b^{\frac12}}} \sqrt[3]{\frac{a}{b}\sqrt{\frac{a}{b}}} \Rightarrow \sqrt[3]{\frac{a}{b}.\frac{a^{\frac12}}{b^{\frac12}}}](/latexrender/pictures/ea24b276823e85d84043e06a76af0e7a.png)

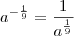 . O mesmo vale para o que está entre parênteses.
. O mesmo vale para o que está entre parênteses.
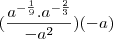
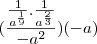
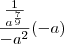

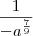
![\frac{a}{\sqrt[9]{-a^7}} \frac{a}{\sqrt[9]{-a^7}}](/latexrender/pictures/1f3b74b1d4f35bd0ac31e68e1f5a8b23.png)

![\sqrt[3]{{\frac{a}{b}}^{\frac{3}{2}}} \sqrt[3]{{\frac{a}{b}}^{\frac{3}{2}}}](/latexrender/pictures/df1b16fd03be1b446154cac49e152b65.png)
![\sqrt[3]{\sqrt[]{{\left( \frac{a}{b} \right)}^{3}}} \sqrt[3]{\sqrt[]{{\left( \frac{a}{b} \right)}^{3}}}](/latexrender/pictures/f02a854bd15f1d2eea4ae842d540c99c.png)
![\sqrt[6]{{\left( \frac{a}{b} \right)}^{3}} \sqrt[6]{{\left( \frac{a}{b} \right)}^{3}}](/latexrender/pictures/3f2aa6945c3a715f3329ce88e7bf4afb.png)

![\sqrt[3]{({\frac{a}{b}})^{\frac{3}{2}}} \sqrt[3]{({\frac{a}{b}})^{\frac{3}{2}}}](/latexrender/pictures/ffd57e44d1b14cc3dc3e0219fa489f20.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.