 por diogenesos » Sex Fev 10, 2012 01:52
por diogenesos » Sex Fev 10, 2012 01:52
(UFRN RN) A solução da equação matricial

é um numero:
a) maior que -1
b) menor que -1
c) maior que 1
d) entre 1 e -1
e) entre 0 e 3.
Não faço ideia de como solucionar a equação, na verdade eu sei o resultado, mas não sei chegar nele.
Se alguém me ajudar com algo passo a passo, agradecerei bastante mesmo !
DOS \\Pré-Vestibulando
-
diogenesos
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Fev 10, 2012 01:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: formado
 por LuizAquino » Sex Fev 10, 2012 11:03
por LuizAquino » Sex Fev 10, 2012 11:03
diogenesos escreveu:(UFRN RN) A solução da equação matricial
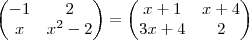
é um numero:
diogenesos escreveu:Não faço ideia de como solucionar a equação, na verdade eu sei o resultado, mas não sei chegar nele.
Para que duas matrizes sejam iguais, todos os seus elementos em posições correspondentes devem ser iguais.
Por exemplo, se A = B, então o elemento

de A é igual ao elemento

de B . De modo geral, se A = B, então o elemento

de A deve ser igual ao elemento
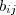
de B.
No caso do exercício, comparando os elementos temos as seguintes equações:
-1 = x + 1
2 = x + 4
x = 3x + 4
x² - 2 = 2
Você deve obter um mesmo valor para x que resolva todas essas equações. Se isso acontecer, então as matrizes serão iguais. Ou seja, a equação matricial terá solução.
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação matricial
por SAAMS » Dom Nov 28, 2010 17:18
- 0 Respostas
- 3685 Exibições
- Última mensagem por SAAMS

Dom Nov 28, 2010 17:18
Matrizes e Determinantes
-
- Equação matricial ????
por thyerry01 » Qui Set 26, 2013 02:06
- 2 Respostas
- 17561 Exibições
- Última mensagem por thyerry01

Sex Set 27, 2013 01:48
Matrizes e Determinantes
-
- (FUVEST) A equação matricial...
por manuoliveira » Seg Set 06, 2010 01:34
- 3 Respostas
- 10500 Exibições
- Última mensagem por rafael_ferramenteiro

Dom Mai 18, 2014 15:05
Matrizes e Determinantes
-
- Calcule o valor de m na equação matricial A*X=B
por andersontricordiano » Seg Jan 16, 2012 19:46
- 3 Respostas
- 3838 Exibições
- Última mensagem por Arkanus Darondra

Qua Jan 18, 2012 23:52
Matrizes e Determinantes
-
- Determinar a matriz X na Equação matricial AX=B
por hugo guedes » Qui Mar 12, 2015 10:37
- 1 Respostas
- 24052 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 25, 2015 16:58
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 de A é igual ao elemento
de A é igual ao elemento  de B . De modo geral, se A = B, então o elemento
de B . De modo geral, se A = B, então o elemento  de A deve ser igual ao elemento
de A deve ser igual ao elemento  de B.
de B.