 por Livia000 » Qua Fev 08, 2012 16:47
por Livia000 » Qua Fev 08, 2012 16:47
Olá,
Seja f(x) = |x-2| + | x-4| + | 2x -6|, para 2?x ?8. Determine a soma do maior e do menor valor de f(x).?
Já tentei resolver a questão acima através do gráfico de f(x), considerando os seguintes casos:
se x maior igual que dois e menor do que três, f(x) = -2x
se x maior igual que 3 e menor do que 4, f(x) = 2x - 4
se x maior igual que 4, f(x)= 4x - 12
Não tenho certeza se essa é a melhor forma de fazê-la.
Minha resposta deu 14...é isso mesmo?
Desde já, agradeço.
-
Livia000
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Fev 08, 2012 16:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por ant_dii » Qua Fev 08, 2012 20:53
por ant_dii » Qua Fev 08, 2012 20:53
Basta que você faça
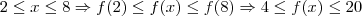
Portanto, a respota correta é 24...
Ops... Você disse menor valor para f no intervalo onde
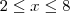
... Então faça como o fraol disse...
Editado pela última vez por
ant_dii em Qua Fev 08, 2012 21:17, em um total de 1 vez.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por fraol » Qua Fev 08, 2012 21:05
por fraol » Qua Fev 08, 2012 21:05
Como estamos tratando de funções lineares dentro dos módulos, num intervalo dado, então podemos analisar os extremos do intervalo dos módulos separadamente, assim:

tem valor 0 para x=2 e
tem valor 6 para x = 8

tem valor 2 para x=2 e
tem valor 4 para x = 8
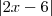
tem valor 2 para x=2 e
tem valor 10 para x = 8
Como você precisa do maior e do menor valor de f(x) no intervalo [2,8], somando o resultado para o extremo 8 você obterá o valor máximo ( a soma dos valores do extremo 2 é menor ).
Resta acharmos o valor mínimo. Aqui podemos usar a propriedade do módulo que diz que o
módulo da soma é sempre menor do que ou igual à soma dos módulos. Traduzindo:
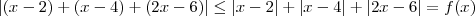
, ou seja:
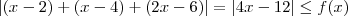
então, por se tratar de módulo o menor valor de f(x) se dará quando

for mínimo, o que ocorre quando
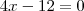
.
Assim você obterá o valor de x que retorna o mínimo de f(x) e poderá terminar o exercício.
Resposta: Menor valor de f(x) = f(3) = 2; Maior valor de f(x) = f(8) = 20; Soma dos valores: 22.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funçao modular
por Fiel8 » Sex Jul 10, 2009 19:25
- 1 Respostas
- 2615 Exibições
- Última mensagem por Molina

Sex Jul 10, 2009 21:50
Funções
-
- Função Modular
 por geriane » Sáb Abr 03, 2010 21:32
por geriane » Sáb Abr 03, 2010 21:32
- 3 Respostas
- 3113 Exibições
- Última mensagem por Molina

Dom Abr 04, 2010 12:57
Funções
-
- Funçao modular
 por Skcedas » Qua Mai 26, 2010 19:29
por Skcedas » Qua Mai 26, 2010 19:29
- 6 Respostas
- 5366 Exibições
- Última mensagem por netlopes

Ter Jun 08, 2010 18:11
Funções
-
- Função Modular
 por DanieldeLucena » Seg Set 20, 2010 18:03
por DanieldeLucena » Seg Set 20, 2010 18:03
- 1 Respostas
- 2243 Exibições
- Última mensagem por MarceloFantini

Seg Set 20, 2010 19:35
Funções
-
- Função Modular
por Pri Ferreira » Ter Nov 22, 2011 18:20
- 1 Respostas
- 1872 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 18:56
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


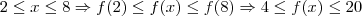
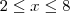 ... Então faça como o fraol disse...
... Então faça como o fraol disse...
 tem valor 0 para x=2 e
tem valor 0 para x=2 e  tem valor 2 para x=2 e
tem valor 2 para x=2 e 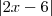 tem valor 2 para x=2 e
tem valor 2 para x=2 e 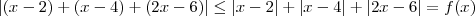 , ou seja:
, ou seja: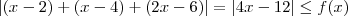 então, por se tratar de módulo o menor valor de f(x) se dará quando
então, por se tratar de módulo o menor valor de f(x) se dará quando  for mínimo, o que ocorre quando
for mínimo, o que ocorre quando 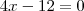 .
. ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.