Fabiana Sa escreveu:1. Se para qualquer y, y pertence ao CD(f), a equação na variável x: f(x)=y tem uma pelo menos uma solução, então f é sobrejetora.
Você já deve saber que uma função é sobrejetora quando o seu contradomínio é igual a sua imagem.
Isso significa que para qualquer y0 que você escolha no contradomínio, haverá
pelo menos um x0 no domínio tal que f(x0) = y0.
Em outras palavras: a equação (em x) dada por f(x)=y tem pelo menos uma solução.
Por exemplo, considere a função

tal que
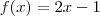
. Escolha um valor y qualquer no contradomínio de f (que é

) . Agora tente resolver a equação (em x) dada por:
2x - 1 = y
Ora, facilmente calculamos que:

Como podemos obter pelo menos essa solução, então f é sobrejetora.
Agora considere a função

tal que
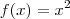
. Escolha um valor y qualquer no contradomínio de f (que é

) . Agora tente resolver a equação (em x) dada por:

Aqui nós teremos um problema! Somente se y for um número positivo ou nulo, que nós podemos escrever:

Note que se y for um número negativo (o que pode acontecer já que os números negativos fazem parte do contradomínio dessa funcão), então não poderíamos encontrar um número x no domínio (que é

) tal que solucionasse a equação.
Portanto, essa função não é sobrejetora.
Fabiana Sa escreveu:2. Se para todo y, y pertence IM(f), a equação na variável x: f(x)=y tem uma única solução, então f é injetora.
Você já deve saber que uma função é injetora quando quaisquer dois elementos distintos do domínio estão associados a dois elementos distintos da imagem.
Isso significa que para qualquer y0 que você escolha na imagem, haverá
somente um x0 no domínio tal que f(x0) = y0.
Em outras palavras: a equação (em x) dada por f(x)=y tem uma única solução.
Por exemplo, considere a função

tal que
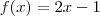
. Escolha um valor y qualquer na imagem de f (que é

) . Agora tente resolver a equação (em x) dada por:
2x - 1 = y
Como já sabemos, uma solução é dada por:

Ora, mas acontece que essa é a única solução possível!
Portanto, a função é injetora.
Agora considere a função

tal que
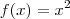
. Escolha um valor y qualquer na imagem de f (que é

) . Agora tente resolver a equação (em x) dada por:

Como y é um número positivo ou nulo, então podemos determinar que:
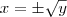
Como há duas soluções, então temos que a função não é injetora.
Fabiana Sa escreveu:3. Se para qualquer y, y pertence CD(f), a equação na variável x: f(x)=y tem uma única soluçao, então f é bijetora.
Você já deve saber que uma função é bijetora quando for ao mesmo tempo injetora e sobrejetora.
Isso significa que para qualquer y0 que você escolha no contradomínio, haverá
somente um x0 no domínio tal que f(x0) = y0.
Em outras palavras: a equação (em x) dada por f(x)=y tem uma única solução.
Por exemplo, considere a função

tal que
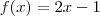
. Escolha um valor y qualquer no contradomínio de f (que é

) . Agora tente resolver a equação (em x) dada por:
2x - 1 = y
Como já sabemos, a única solução é dada por:

Portanto, a função é bijetora.
Agora considere a função

tal que
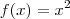
. Escolha um valor y qualquer no contradomínio de f (que é

) . Agora tente resolver a equação (em x) dada por:

Como sabemos, essa equação pode não ter solução (quando y for negativo), ter apenas uma solução (quando y for zero) ou ter duas soluções distintas (quando y for positivo). Em resumo: dependendo do y escolhido no contradomínio, a solução pode não ser única.
Portanto, essa função não é bijetora.


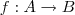 é injetora quando para quaisquer elementos
é injetora quando para quaisquer elementos  e
e  de A (Domínio),
de A (Domínio),  implica
implica  . Em outras palavras, quando
. Em outras palavras, quando  , em A, implica
, em A, implica em B (Contradomínio).
em B (Contradomínio). , existe pelo menos um
, existe pelo menos um 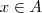 tal que
tal que 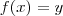 .
.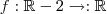 definida por
definida por  não é sobrejetora, veja que o ponto P não esta sobre o gráfico:
não é sobrejetora, veja que o ponto P não esta sobre o gráfico: definida por
definida por  é sobrejetora. Observe que a imagem é todo o contradomínio:
é sobrejetora. Observe que a imagem é todo o contradomínio: , então
, então e
e 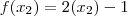 implicam que
implicam que 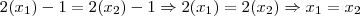 , portanto f é injetora.
, portanto f é injetora.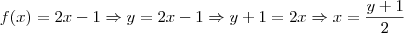

 , mas isso fica de exercício pra você...
, mas isso fica de exercício pra você...
 tal que
tal que 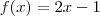 . Escolha um valor y qualquer no contradomínio de f (que é
. Escolha um valor y qualquer no contradomínio de f (que é  ) . Agora tente resolver a equação (em x) dada por:
) . Agora tente resolver a equação (em x) dada por:
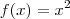 . Escolha um valor y qualquer no contradomínio de f (que é
. Escolha um valor y qualquer no contradomínio de f (que é 

 ) . Agora tente resolver a equação (em x) dada por:
) . Agora tente resolver a equação (em x) dada por: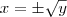

 Estou resolvendo provas de anos anteriores das universidades daqui da Bahia (principalmente as estaduais e federais ) e conto com a ajuda de vcs para qualquer dificuldade nas resoluções das questões
Estou resolvendo provas de anos anteriores das universidades daqui da Bahia (principalmente as estaduais e federais ) e conto com a ajuda de vcs para qualquer dificuldade nas resoluções das questões  !
!