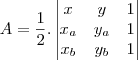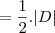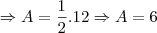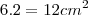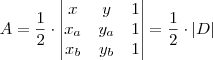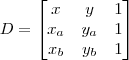por natanlp » Qua Fev 01, 2012 00:45
por natanlp » Qua Fev 01, 2012 00:45
Olá Pessoal, Gostaria da ajuda de vocês, pois durante todo meu ensino médio nunca ouvi falar de Geometria Analitica, Fiz uma prova recentemente, e caiu a questão abaixo, como faço para resolver a mesma? pois não tenho a menor idéia de como fazer, e gostaria tbm que se pudessem, me endicassem algum material para estudo, Desde já agradeço!!!
Um agricultor recebeu como herança um sítio em formato retangular com
vértices A, B, C e D. Em sua representação no plano cartesiano, em que a
unidade em cada um dos eixos representa a unidade de comprimento sobre o
terreno, tem-se A(4,0), B(6,2), C(2,4) e D(0,2). Quantas unidades de
área possui o sítio que o agricultor herdou?
a) 12
b) 13
c) 14
d) 24
-
natanlp
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Fev 01, 2012 00:40
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso técnico em Informática
- Andamento: formado
 por Arkanus Darondra » Qua Fev 01, 2012 10:48
por Arkanus Darondra » Qua Fev 01, 2012 10:48
Olá Natan!
Creio que nenhuma das alternativas seja a resposta, ou, então, houve algum erro na digitação da questão.
Para resolver esta questão basta que você encontre a medida dos dois lado do retângulo, e multiplique-as.
Isso é possível encontrando a distancia entre dois pontos:




e

terão as mesmas medidas de

e

, respectivamente. (Faça o desenho para comprovar).
Desse modo a área do terreno será


-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por natanlp » Qua Fev 01, 2012 11:20
por natanlp » Qua Fev 01, 2012 11:20
Olá Arkanus Darondra, obrigado pela atenção!
O Gabarito da prova em questão informa que a resposta é a letra (a) 12...
fecha 2 triangulos imagina os vertices A e B com C e D paralelos
fecha o triangulo ABC e CDA
faz o det dos vertices divide por 2 e soma as areas
4 6 2 4
0 2 4 0 = det(ABC)
2 0 4 2
4 2 0 4 = det(CDA)
|det(abc)|/2 + |det(cda)|/2 = Area total
2 0 4 2
4 2 0 4
2.2 + 0.0 +4.4 -2.0 -4.2 -0.4 = 12
Eu já recebi a seguinte sugestão para a solução do mesmo...
mas quem me informou esta sugestão se limitou a informar que
"aquela matriz ali eu aprendi a fazer com meu professor , nao tenho como provar , mas da certo"
Então se alguem mais, tiver alguma explicação para a sugestão apresentada acima, Ficarei grato!
-
natanlp
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Fev 01, 2012 00:40
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso técnico em Informática
- Andamento: formado
 por natanlp » Qua Fev 01, 2012 12:29
por natanlp » Qua Fev 01, 2012 12:29
Obrigado Arkanus Darondra,
Essa sua resolução eu consegui entender..
Valeu!!
-
natanlp
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Fev 01, 2012 00:40
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso técnico em Informática
- Andamento: formado
 por Arkanus Darondra » Qua Fev 01, 2012 14:40
por Arkanus Darondra » Qua Fev 01, 2012 14:40
Natan, como você pôde perceber no outro fórum, essa minha resolução só é válida se o enunciado dissesse que o sítio é
quadrangular, ao invés de
retangular.
Isso porque os pontos, de fato, não formam um retângulo, e sim um paralelogramo.
Portanto, a questão está incorreta, e minha resolução e o gabarito são válidos apenas se considerarmos o detalhe anterior.

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Qua Fev 01, 2012 14:59
por LuizAquino » Qua Fev 01, 2012 14:59
natanlp escreveu:(...) gostaria tbm que se pudessem, me endicassem algum material para estudo (...)
Eu recomendo que você assista as vídeo-aulas do Nerckie:
http://www.youtube.com/nerckieArkanus Darondra escreveu:Há uma fórmula para calcular a área de uma triângulo por meio das coordenadas:
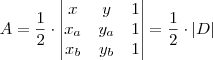
Cuidado para não confundir as barras verticais que indicam determinante, com as barras verticais que indicam módulo.
Para não haver essa confusão, primeiro escreva a matriz:
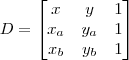
Em seguida, escreva a fórmula:

Editado pela última vez por
LuizAquino em Qua Fev 01, 2012 15:09, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por natanlp » Qua Fev 01, 2012 15:08
por natanlp » Qua Fev 01, 2012 15:08
Olá Arkanus Darondra
A área em apreço não é totalmente retângular é losangonal.
http://pt.wikipedia.org/wiki/LosangoA = D1 * D2 / 2
Assim é necessario calcular as distâncias entre os pontos C e A ; e B e D, multiplicá-las e dividir por dois
Obrigado pela ajuda...
-
natanlp
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Fev 01, 2012 00:40
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso técnico em Informática
- Andamento: formado
 por LuizAquino » Qua Fev 01, 2012 15:12
por LuizAquino » Qua Fev 01, 2012 15:12
natanlp escreveu:A área em apreço não é totalmente retângular é losangonal.
Você está enganado. Não é um losango. Note que um losango possui os quatro lados com o mesmo comprimento. Esse não é o caso da área em questão.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Arkanus Darondra » Qua Fev 01, 2012 15:34
por Arkanus Darondra » Qua Fev 01, 2012 15:34
LuizAquino escreveu:Cuidado para não confundir as barras verticais que indicam determinante, com as barras verticais que indicam módulo.
Para não haver essa confusão, primeiro escreva a matriz:
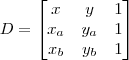
Em seguida, escreva a fórmula:

Tem razão. Obrigado.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integrais - calcular unidades de área
por soraaxs » Sáb Nov 30, 2013 22:41
- 4 Respostas
- 3219 Exibições
- Última mensagem por soraaxs

Qua Dez 04, 2013 01:32
Cálculo: Limites, Derivadas e Integrais
-
- Calcular área
por Anakinrj » Ter Nov 23, 2010 21:33
- 8 Respostas
- 5747 Exibições
- Última mensagem por Moura

Ter Dez 14, 2010 06:58
Cálculo: Limites, Derivadas e Integrais
-
- Calcular área
por Anakinrj » Qua Nov 24, 2010 12:11
- 2 Respostas
- 2283 Exibições
- Última mensagem por Moura

Ter Dez 14, 2010 07:44
Cálculo: Limites, Derivadas e Integrais
-
- Calcular área
por pedcoi » Qui Fev 02, 2012 11:19
- 2 Respostas
- 2039 Exibições
- Última mensagem por pedcoi

Sex Fev 03, 2012 14:03
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL]Calcular área y=x^2
 por krtc » Qua Jul 24, 2013 02:07
por krtc » Qua Jul 24, 2013 02:07
- 5 Respostas
- 3707 Exibições
- Última mensagem por Russman

Qua Jul 24, 2013 03:13
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 e
e  terão as mesmas medidas de
terão as mesmas medidas de  e
e  , respectivamente. (Faça o desenho para comprovar).
, respectivamente. (Faça o desenho para comprovar).