 por angels900 » Ter Jan 31, 2012 14:35
por angels900 » Ter Jan 31, 2012 14:35
- Escreva as equações paramétricas da reta
 que passa pelos pontos
que passa pelos pontos 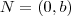 e
e  do plano.
do plano. - Determine as coordenadas dos pontos de interseção da elipse
 de equação
de equação  com a reta
com a reta  obtida no item a.
obtida no item a. - Escreva as equações paramétricas da reta
 que passa pelo ponto
que passa pelo ponto 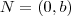 e pelo ponto
e pelo ponto  de
de  , com
, com  .
. - Para
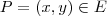 , com
, com  , determine
, determine  , sendo
, sendo  o ponto de interseção da reta
o ponto de interseção da reta  , obtida no item c, com o eixo das abcissas.
, obtida no item c, com o eixo das abcissas. - Mostre que a função
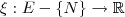 , definida por
, definida por 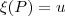 , com
, com  obtido no item d, estabelece uma correspondência biunívoca entre
obtido no item d, estabelece uma correspondência biunívoca entre  e
e 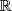 .
. - Determine a expressão de
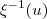 , sendo
, sendo 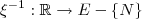 a função inversa da função
a função inversa da função  do item e.
do item e.
-
angels900
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Jan 30, 2012 05:02
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
 por LuizAquino » Ter Jan 31, 2012 14:42
por LuizAquino » Ter Jan 31, 2012 14:42
angels900,
Por favor, poste as suas tentativas e indique exatamente onde está a sua dúvida.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por angels900 » Ter Jan 31, 2012 14:54
por angels900 » Ter Jan 31, 2012 14:54
eu acho que a reta eh

mas nao sei oque eh equacao parametrica entao parei ae
-
angels900
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Jan 30, 2012 05:02
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
 por LuizAquino » Ter Jan 31, 2012 14:57
por LuizAquino » Ter Jan 31, 2012 14:57
angels900 escreveu:mas nao sei oque eh equacao parametrica entao parei ae
Leia a página abaixo e tente terminar.
Equações paramétricashttp://www.mundoeducacao.com.br/matemat ... tricas.htm
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por angels900 » Ter Jan 31, 2012 15:01
por angels900 » Ter Jan 31, 2012 15:01
mas a reta eh essa mesmo?
-
angels900
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Jan 30, 2012 05:02
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
 por angels900 » Ter Jan 31, 2012 15:21
por angels900 » Ter Jan 31, 2012 15:21
quais sao as equacoes parametricas desta equacao
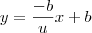
nao entendi como achar
-
angels900
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Jan 30, 2012 05:02
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
 por LuizAquino » Ter Jan 31, 2012 17:04
por LuizAquino » Ter Jan 31, 2012 17:04
angels900 escreveu:mas a reta eh essa mesmo?
eu acho que a reta eh

Sim, esta é a reta do item a).
angels900 escreveu:quais sao as equacoes parametricas desta equacao

nao entendi como achar
Comece chamando x de t. Isto é, faça a substituição x=t. Desse modo, temos que

.
Portanto, uma equação paramétrica dessa reta é dada por:
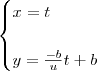
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações cartesianas e equações paramétricas
por Victor Mello » Sáb Ago 23, 2014 16:24
- 1 Respostas
- 3423 Exibições
- Última mensagem por Russman

Sáb Ago 23, 2014 18:29
Funções
-
- Equações paramétricas da curva
por kalschne » Qui Fev 16, 2012 20:51
- 3 Respostas
- 2109 Exibições
- Última mensagem por kalschne

Qui Fev 16, 2012 22:48
Geometria Analítica
-
- [Equações Paramétricas - Espaço]
por raimundoocjr » Ter Set 24, 2013 20:40
- 2 Respostas
- 1859 Exibições
- Última mensagem por raimundoocjr

Qua Set 25, 2013 19:05
Cálculo: Limites, Derivadas e Integrais
-
- Faz sentido? Sistema e equações paramétricas.
por Dan » Ter Fev 01, 2011 14:39
- 4 Respostas
- 3752 Exibições
- Última mensagem por LuizAquino

Qua Fev 02, 2011 11:37
Sistemas de Equações
-
- Geometria Analítica Equações Paramétricas.
por lucat28 » Sex Set 16, 2011 19:08
- 1 Respostas
- 1404 Exibições
- Última mensagem por MarceloFantini

Sex Set 16, 2011 19:43
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 que passa pelos pontos
que passa pelos pontos 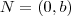 e
e  do plano.
do plano. de equação
de equação  com a reta
com a reta  obtida no item a.
obtida no item a. que passa pelo ponto
que passa pelo ponto 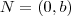 e pelo ponto
e pelo ponto  de
de  , com
, com  .
.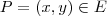 , com
, com  , determine
, determine  , sendo
, sendo  o ponto de interseção da reta
o ponto de interseção da reta  , obtida no item c, com o eixo das abcissas.
, obtida no item c, com o eixo das abcissas.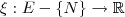 , definida por
, definida por 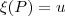 , com
, com  obtido no item d, estabelece uma correspondência biunívoca entre
obtido no item d, estabelece uma correspondência biunívoca entre  e
e 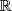 .
.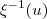 , sendo
, sendo 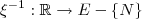 a função inversa da função
a função inversa da função  do item e.
do item e.



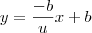
 .
.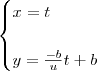

 .
.
 :
: