Toda vez que um evento ocorre, ele tem 51.35% de probabilidade de chegar no resultado A.
Esse evento ocorrerá 1024 vezes. Qual a probabilidade de que, em toda esta série, exista uma sequência de pelo menos 9 vezes consecutivas em que não foi obtido o resultado A?
(Desculpem pelos números quebrados, trata-se de um problema real. Caso queiram simplificar as variáveis tudo bem, mas deixem a maneira de resolução para que eu possa chegar ao resultado do problema com estas variáveis, obrigado).


 a probabilidade de obter-se o resultado A.
a probabilidade de obter-se o resultado A. a probabilidade de não obter-se o resultado A.
a probabilidade de não obter-se o resultado A.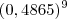 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.