


cris_leite escreveu:Gostaria de saber qual é a probabilidade de, numa equipa com seis elementos, 4 rapazes e 2 raparigas, ser escolhida uma equipa de dois elementos formada apenas por rapazes
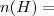 equipe composta por dois homens,
equipe composta por dois homens,  número total de equipes,
número total de equipes, 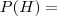 probabilidade desejada, temos:
probabilidade desejada, temos:
 40%
40%




cris_leite escreveu:Mas o número de casos possíveis quando utilizo combinações de 6, 2 a 2 é 15 e o número de casos possíveis quando utilizo 4/6 x3/5 é 30, o que não é igual. Daí a minha dúvida se posso calcular a probabilidade das duas formas.
 .
. 

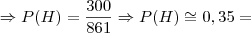 35%
35%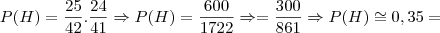 35%
35%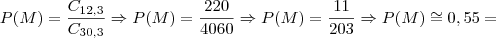 55%
55%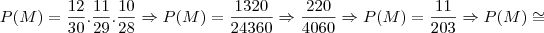 55%
55%

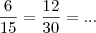 , e aqui não há o que discutir.
, e aqui não há o que discutir. - plicidade " a ser descontada - mas isso já é outra conversa...)
- plicidade " a ser descontada - mas isso já é outra conversa...)


Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
