 por Ana_Rodrigues » Qui Jan 26, 2012 18:54
por Ana_Rodrigues » Qui Jan 26, 2012 18:54
Quero saber por que

oscila entre 1 e -1
Por que o período do gráfico do seno diminui a medida que x se aproxima de zero?
Agradeço desde já a quem me ajudar a entender!
-
Ana_Rodrigues
- Usuário Parceiro

-
- Mensagens: 51
- Registrado em: Seg Nov 14, 2011 09:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fraol » Qui Jan 26, 2012 19:36
por fraol » Qui Jan 26, 2012 19:36
Vamos analisar um pouco o caso da oscilação.
Antes de mais nada, não se pode falar que o
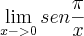
oscila entre 1 e -1, uma vez que este limite não existe, se existisse não estaria oscilando, a função oscila.
A oscilação ocorre pois

cresce ilimitadamente quando x tende a 0 ( ou descresce ilimitadamente no caso de x tender a zero pela esquerda ).
Em qualquer caso, haverá inúmeros casos de x que tornam

um número múltiplo de

ou múltiplo de
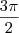
, casos em que o seno é 1 e -1 respectivamente.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Ana_Rodrigues » Qui Jan 26, 2012 20:00
por Ana_Rodrigues » Qui Jan 26, 2012 20:00
Eu entendi a resposta, mas ainda tenho dúvida quanto ao gráfico!
Tipo numa ilustração aqui no livro os períodos perto de zero são bem pequenos. Sendo que a condição para que um gráfico seja comprimido horizontalmente é: y=f(cx).
-
Ana_Rodrigues
- Usuário Parceiro

-
- Mensagens: 51
- Registrado em: Seg Nov 14, 2011 09:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fraol » Qui Jan 26, 2012 20:47
por fraol » Qui Jan 26, 2012 20:47
Analisando o período da função, com base nessa abordagem mais comum do coeficiente que multiplica a variável x, poderíamos supor que a função
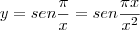
e aí teríamos que o coeficiente de x é
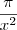
, que descresce mais e mais à medida que x tende a 0. Na verdade, estamos tratando de uma função caótica.
Prefiro analisar assim:

tem grandes incrementos no seu valor quando fazemos x tender a 0, mesmo lentamente. Em outras palavras, a função oscila rapidamente à medida que x se aproxima de 0. Assim sua frequência aumenta rapidamente. Como o Período é o inverso da Frequência, temos que o período diminui rapidamente.
(editando para concluir)
Isso explica por que o gráfico tem linhas cada vez maiz próximas ( período pequeno ) e em uma quantidade muito grande ( frequência grande ).
É isso.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Ana_Rodrigues » Sex Jan 27, 2012 14:28
por Ana_Rodrigues » Sex Jan 27, 2012 14:28
Obrigada!
-
Ana_Rodrigues
- Usuário Parceiro

-
- Mensagens: 51
- Registrado em: Seg Nov 14, 2011 09:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6644 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4790 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5119 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7259 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4436 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 oscila entre 1 e -1
oscila entre 1 e -1
 oscila entre 1 e -1
oscila entre 1 e -1
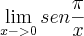 oscila entre 1 e -1, uma vez que este limite não existe, se existisse não estaria oscilando, a função oscila.
oscila entre 1 e -1, uma vez que este limite não existe, se existisse não estaria oscilando, a função oscila. cresce ilimitadamente quando x tende a 0 ( ou descresce ilimitadamente no caso de x tender a zero pela esquerda ).
cresce ilimitadamente quando x tende a 0 ( ou descresce ilimitadamente no caso de x tender a zero pela esquerda ).  um número múltiplo de
um número múltiplo de  ou múltiplo de
ou múltiplo de 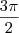 , casos em que o seno é 1 e -1 respectivamente.
, casos em que o seno é 1 e -1 respectivamente.

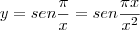 e aí teríamos que o coeficiente de x é
e aí teríamos que o coeficiente de x é 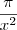 , que descresce mais e mais à medida que x tende a 0. Na verdade, estamos tratando de uma função caótica.
, que descresce mais e mais à medida que x tende a 0. Na verdade, estamos tratando de uma função caótica. tem grandes incrementos no seu valor quando fazemos x tender a 0, mesmo lentamente. Em outras palavras, a função oscila rapidamente à medida que x se aproxima de 0. Assim sua frequência aumenta rapidamente. Como o Período é o inverso da Frequência, temos que o período diminui rapidamente.
tem grandes incrementos no seu valor quando fazemos x tender a 0, mesmo lentamente. Em outras palavras, a função oscila rapidamente à medida que x se aproxima de 0. Assim sua frequência aumenta rapidamente. Como o Período é o inverso da Frequência, temos que o período diminui rapidamente.






