![\sqrt[]{1+x+{x}^{2}} \sqrt[]{1+x+{x}^{2}}](/latexrender/pictures/5458ff43753bc8f70c5c1a9f4f333f9d.png)
![+\sqrt[]{1-x+{x}^{2}} +\sqrt[]{1-x+{x}^{2}}](/latexrender/pictures/a9dd9a67df80168aba8f55330aabbdd9.png) =4
=4Elevei ambos os lados ao quadrado e encontrei:
 +x+1=16-8
+x+1=16-8![\sqrt[]{{x}^{2}-x+1}+{x}^{2}-x+1 \sqrt[]{{x}^{2}-x+1}+{x}^{2}-x+1](/latexrender/pictures/63fdc3a90922f70c5e73324f92f753e1.png)

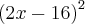 =
=![\left({-8\sqrt[]{{x}^{2}-x+1}} \right)^{2} \left({-8\sqrt[]{{x}^{2}-x+1}} \right)^{2}](/latexrender/pictures/572d8dd31234b7bb68e825eb55fac26c.png)
 4x-64x+256=64
4x-64x+256=64 -64x+64
-64x+64 64
64 -4x-192=0
-4x-192=0Eu fiz assim, porém resolvendo a equação eu nao encontro como resultado um valor igual a resposta do livro que é 4/
![\sqrt[]{5}, -4/\sqrt[]{5} \sqrt[]{5}, -4/\sqrt[]{5}](/latexrender/pictures/e0cf2fc8f2e958292c2bd6f9a4b85424.png)
Se alguem puder me ajudar...

![\sqrt[]{1+x+{x}^{2}} \sqrt[]{1+x+{x}^{2}}](/latexrender/pictures/5458ff43753bc8f70c5c1a9f4f333f9d.png)
![+\sqrt[]{1-x+{x}^{2}} +\sqrt[]{1-x+{x}^{2}}](/latexrender/pictures/a9dd9a67df80168aba8f55330aabbdd9.png) =4
=4 +x+1=16-8
+x+1=16-8![\sqrt[]{{x}^{2}-x+1}+{x}^{2}-x+1 \sqrt[]{{x}^{2}-x+1}+{x}^{2}-x+1](/latexrender/pictures/63fdc3a90922f70c5e73324f92f753e1.png)

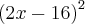 =
=![\left({-8\sqrt[]{{x}^{2}-x+1}} \right)^{2} \left({-8\sqrt[]{{x}^{2}-x+1}} \right)^{2}](/latexrender/pictures/572d8dd31234b7bb68e825eb55fac26c.png)
 4x-64x+256=64
4x-64x+256=64 -64x+64
-64x+64 64
64 -4x-192=0
-4x-192=0![\sqrt[]{5}, -4/\sqrt[]{5} \sqrt[]{5}, -4/\sqrt[]{5}](/latexrender/pictures/e0cf2fc8f2e958292c2bd6f9a4b85424.png)

nathyn escreveu:![{\left(2x-16 \right)}^{2}=\left({-8\sqrt[]{{x}^{2}-x+1}} \right)^{2}\Rightarrow {\left(2x-16 \right)}^{2}=\left({-8\sqrt[]{{x}^{2}-x+1}} \right)^{2}\Rightarrow](/latexrender/pictures/f2a755df3fe8582de15a54f63dfe568d.png)


Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)