 por moyses » Qua Jan 25, 2012 09:48
por moyses » Qua Jan 25, 2012 09:48
eis aqui outra pergunta:
12 (UFU-MG) Sejam
A,
B e
C três conjuntos em um universo
U. Qual a alternativa falsa, dentre as seguites Relacionadas?
A)

B)

C)

D)

E)

e ai gente qual Vocês acham que é? Eu acho que é a letra C)

a falsa, mais eu to meu com duvida na letra A)

.... me ajudem fazendo favor e me responda o por que de cada letra ai fazendo favor... valew gente

OBS: Eu não consigui interpretar a letra A), mais eu acho que é ela só que eu não sei responder logicamente , me ajudem kkkk

-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por ant_dii » Qua Jan 25, 2012 13:02
por ant_dii » Qua Jan 25, 2012 13:02
moyses escreveu:A)

Supondo que
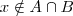
, então

ou

. Outra forma de dizer isto é:
se

, então
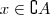
ou
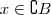
Formalmente e resumidamente (pois existem alguns detalhes relativos),

Quanto
moyses escreveu:B)

C)

Em B), vemos que se

, então
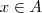
ou

. Mas, se
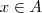
, então

ou se

, então
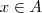
e
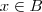
,de onde
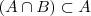
. Portanto

Em C), supondo que
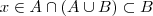
, então
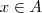
e

, de onde
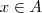
... A não ser que

, não há como garantir que
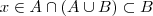
.
As letras D) e E), você encontrará a demonstração na literatura. Portanto, a única que apresenta incoerência e a letra C mesmo...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por moyses » Qua Jan 25, 2012 13:32
por moyses » Qua Jan 25, 2012 13:32
beleza valew ant_dii, mais teria como você exclicar esse "detalhes relativos" ou seria muito confuso pra eu enteder? sei lá depende , ta vendo eu acertei essa questão, dessa vez eu analizei com calma

muita mesmo kkkk. Mias voltando tem como você exclicar esse detalhes da letra A) e por que A) é correto? fazendo favor kkk

-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por ant_dii » Qua Jan 25, 2012 14:38
por ant_dii » Qua Jan 25, 2012 14:38
Na verdade, eu pensei bem e não haverá detalhes... É que na hora em que enviei pensei que fosse necessário provar o que estava escrito, mas não é necessário. O que fiz foi somente reescrever a afirmação... Esses detalhes que falei são de como provar que dois conjuntos são iguais e é necessário provar que

, pois não é tão óbvio...
Mas fique tranquilo, é fácil e para o que vc precisa seria desnecessário...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por moyses » Qui Jan 26, 2012 13:11
por moyses » Qui Jan 26, 2012 13:11
tudo bem, mais eu gosto

deles, pois são eles que são a base pra você contruir a logica... Eu tabem estou interresado em fazer uma graduação em matemática tabem!!!

.... mais valew por enquanto , você me ajudou muitissimo... Outra coisa que eu percebi nessa igualdade é que foi feito uma distributiva semelhante a uma multiplicação e isso é bacana.. até mais valeww


-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teoria dos conjuntos, Pergunta de lógica
por moyses » Dom Jan 22, 2012 16:53
- 9 Respostas
- 5908 Exibições
- Última mensagem por moyses

Qua Jan 25, 2012 08:51
Álgebra Elementar
-
- Cunjutos Numericos ; Pergunta de logica
por moyses » Qua Jan 18, 2012 14:03
- 5 Respostas
- 3690 Exibições
- Última mensagem por moyses

Qui Jan 19, 2012 21:40
Conjuntos
-
- Outra Dúvida - Conjuntos
por joaopedrel » Dom Mar 14, 2010 20:03
- 2 Respostas
- 1672 Exibições
- Última mensagem por joaopedrel

Dom Mar 14, 2010 22:57
Conjuntos
-
- [Lógica formal] Mostrar que é um teorema do sistema dedutivo
 por fff » Sáb Fev 07, 2015 09:32
por fff » Sáb Fev 07, 2015 09:32
- 0 Respostas
- 1502 Exibições
- Última mensagem por fff

Sáb Fev 07, 2015 09:32
Lógica
-
- Conjuntos - Questão de lógica
por juno » Ter Jan 24, 2012 13:42
- 2 Respostas
- 2524 Exibições
- Última mensagem por juno

Ter Jan 24, 2012 15:17
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 a falsa, mais eu to meu com duvida na letra A)
a falsa, mais eu to meu com duvida na letra A) .... me ajudem fazendo favor e me responda o por que de cada letra ai fazendo favor... valew gente
.... me ajudem fazendo favor e me responda o por que de cada letra ai fazendo favor... valew gente 


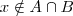 , então
, então  ou
ou  . Outra forma de dizer isto é:
. Outra forma de dizer isto é: , então
, então 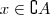 ou
ou 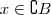

 , então
, então 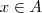 ou
ou  . Mas, se
. Mas, se  ou se
ou se 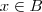 ,de onde
,de onde 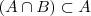 . Portanto
. Portanto 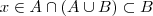 , então
, então  , de onde
, de onde  , não há como garantir que
, não há como garantir que 
 muita mesmo kkkk. Mias voltando tem como você exclicar esse detalhes da letra A) e por que A) é correto? fazendo favor kkk
muita mesmo kkkk. Mias voltando tem como você exclicar esse detalhes da letra A) e por que A) é correto? fazendo favor kkk 





