 por lourivallobo » Ter Jan 24, 2012 20:47
por lourivallobo » Ter Jan 24, 2012 20:47
Se y=log81(1/27) e x ? IR+ são tais que xy= 8 , e
x é igual a
a) 1/16
b) ½
c) Log3 8
d) 2
e) 16
- Anexos
-
[O anexo não pode ser exibido, pois a extensão pdf foi desativada pelo administrador.]
-
lourivallobo
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Jan 24, 2012 20:38
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Telecomunicações
- Andamento: formado
 por LuizAquino » Ter Jan 24, 2012 21:12
por LuizAquino » Ter Jan 24, 2012 21:12
lourivallobo escreveu:Se y=log81(1/27) e x ? IR+ são tais que xy= 8 , e
x é igual a
a) 1/16
b) ½
c) Log3 8
d) 2
e) 16
Analisando a prova que você postou, a questão na verdade é:
Se
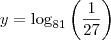
e
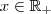
são tais que

, então
x é igual a
a) 1/16
b)1/2
c)

d) 2
e) 16
Note que:
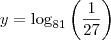
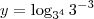
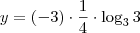
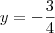
Sendo assim, temos que:
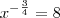
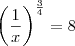
![\frac{1}{x} = \sqrt[3]{8^4} \frac{1}{x} = \sqrt[3]{8^4}](/latexrender/pictures/4f58a5f9b27ecc55f84967d12822e058.png)
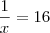

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Concurso Petrobras
por lourivallobo » Ter Jan 24, 2012 20:49
- 1 Respostas
- 1446 Exibições
- Última mensagem por LuizAquino

Ter Jan 24, 2012 21:51
Estatística
-
- Concurso Petrobras
por lourivallobo » Ter Jan 24, 2012 20:52
- 1 Respostas
- 3011 Exibições
- Última mensagem por LuizAquino

Ter Jan 24, 2012 22:08
Estatística
-
- Concurso Petrobras
 por lourivallobo » Qua Jan 25, 2012 09:13
por lourivallobo » Qua Jan 25, 2012 09:13
- 4 Respostas
- 2986 Exibições
- Última mensagem por Arkanus Darondra

Qua Jan 25, 2012 17:30
Matrizes e Determinantes
-
- PA concurso petrobras
por thiagodr » Sex Mar 23, 2012 01:07
- 3 Respostas
- 2003 Exibições
- Última mensagem por thiagodr

Sáb Abr 07, 2012 16:34
Progressões
-
- DERIVADA - CONCURSO PETROBRAS
por pinkfluor » Qua Mar 02, 2011 11:10
- 2 Respostas
- 2319 Exibições
- Última mensagem por LuizAquino

Qua Mar 02, 2011 12:06
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



e
são tais que
, então
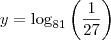
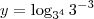
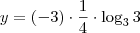

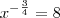
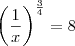
![\frac{1}{x} = \sqrt[3]{8^4} \frac{1}{x} = \sqrt[3]{8^4}](/latexrender/pictures/4f58a5f9b27ecc55f84967d12822e058.png)
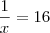


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.