 por onorax » Ter Jan 24, 2012 00:24
por onorax » Ter Jan 24, 2012 00:24
Ola, bem eu preciso fazer um trabalho para meu curso de programação no qual o programa de o tempo que ira demorar um dowload
eu tenho que fazer assim:
o programa pede"Kilobit por segundo", e tamanho do arquivo em KB(kilobyte), e o programa de o tempo
o programa pede"Kilobit por segundo", e tamanho do arquivo em MB(megabyte), e o programa de o tempo
o programa pede"Kilobit por segundo", e tamanho do arquivo em GB(gigabyte), e o programa de o tempo
eu sei que, 1 kilobit é = a, 0.125KB e 0.0001220703125MB
e 1GB é = a 8388608Kilobit
OBS: note a diferença entre kilob
ite(K
b) e kilob
yte(K
B), um conversor de bit:
http://www.gwebtools.com.br/converter-bitvou postar uma foto do programa só para que entendam melhor, tem a segunda parte e vou precisar de formulas ai eu posto aqui pedindo ajuda porque sou uma negação com formula, enchi a folha do caderno e quase n fiz evolução

ali em Kbps tem tb MB mais isso vou deixar para depois que fizer com Kbps
-
onorax
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Jan 24, 2012 00:09
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Programação
- Andamento: cursando
 por LuizAquino » Ter Jan 24, 2012 19:11
por LuizAquino » Ter Jan 24, 2012 19:11
onorax escreveu:Ola, bem eu preciso fazer um trabalho para meu curso de programação no qual o programa de o tempo que ira demorar um dowload
Prezado
onorax, gostaria de deixar claro que
não é objetivo do fórum resolver trabalhos ou listas de exercício.
Dito isso, eu vou apenas indicar os passos que você deve seguir para calcular o tempo de download dado a velocidade (em Kbps) e o tamanho do arquivo (em KB).
Passo 1) Converta a velocidade de Kbps para KB/s. Para isso, basta dividir a velocidade em Kbps por 8.
Exemplo: Considere que a velocidade é 128 Kbps. Efetuando a divisão, temos que
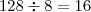
. Portanto, temos que 128 Kbps é equivalente a 16 KB/s.
Passo 2) Divida o tamanho em KB pela velocidade em KB/s. Isso irá fornecer o tempo (em segundos) para realizar o download;
Exemplo: Considere que o tamanho é 120 KB e que a velocidade é 16 KB/s. Efetuando a divisão, temos que

. Portanto, temos que o tempo é de 7,5 segundos.
Agora tente modificar esses passos para tamanhos em MB ou GB.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Conversão de Unidades
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



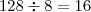 . Portanto, temos que 128 Kbps é equivalente a 16 KB/s.
. Portanto, temos que 128 Kbps é equivalente a 16 KB/s. . Portanto, temos que o tempo é de 7,5 segundos.
. Portanto, temos que o tempo é de 7,5 segundos.





