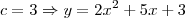<boa noite,
agradecia informações sobre como descobrir a equação que está representada através de uma parábola/gráfico da função. Consigo escrever o gráfico da função tendo informação sobre a equação (ex: y = 2x^2+5x+3), no entanto gostaria de saber como fazer o inverso olhando apenas para o gráfico da função.
Obrigado,
Ricardo



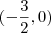 e
e  , e, em y
, e, em y 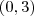 . Além disso,
. Além disso, 


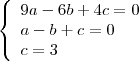
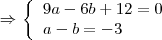
 ,
,  e
e