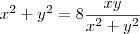por luiz_henriquear » Sáb Jan 21, 2012 13:30
por luiz_henriquear » Sáb Jan 21, 2012 13:30
Boa Tarde.
Gostaria da ajuda para a equação polar
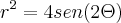
A dúvida é quanto ao 2 que multiplica o theta.
att.
Luiz
-
luiz_henriquear
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Seg Out 24, 2011 20:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia civil
- Andamento: cursando
 por LuizAquino » Sáb Jan 21, 2012 13:54
por LuizAquino » Sáb Jan 21, 2012 13:54
luiz_henriquear escreveu:Gostaria da ajuda para a equação polar
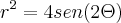
A dúvida é quanto ao 2 que multiplica o theta.
Qual é exatamente a sua dúvida sobre ele?
Além disso, qual é o objetivo do exercício? Seria esboçar o gráfico dessa curva?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por luiz_henriquear » Sáb Jan 21, 2012 14:28
por luiz_henriquear » Sáb Jan 21, 2012 14:28
o exercício pede que se transforme de equação polar para equação cartesiana. Quanto ao dois a dúvida seria o que fazer com ele na substituição
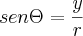
-
luiz_henriquear
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Seg Out 24, 2011 20:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia civil
- Andamento: cursando
 por ant_dii » Sáb Jan 21, 2012 17:41
por ant_dii » Sáb Jan 21, 2012 17:41
Use o fato de que
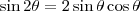
.
Então

Usando o fato de que

e
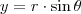
, onde
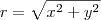
, você encontrará que
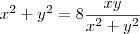
Agora basta manipular...
Se não ficou tão simples avise...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por luiz_henriquear » Sáb Jan 21, 2012 18:59
por luiz_henriquear » Sáb Jan 21, 2012 18:59
oh loko!! mais mole que torcer pro barcelona.
-
luiz_henriquear
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Seg Out 24, 2011 20:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia civil
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Numeros Complexos] Forma polar e cartesiana de w1 e w2
por karenfreitas » Dom Dez 04, 2016 16:36
- 0 Respostas
- 5248 Exibições
- Última mensagem por karenfreitas

Dom Dez 04, 2016 16:36
Números Complexos
-
- Expressão Cartesiana de um Vetor
por davidufpe » Sáb Out 25, 2014 21:55
- 1 Respostas
- 2836 Exibições
- Última mensagem por adauto martins

Seg Out 27, 2014 14:25
Geometria Analítica
-
- determinado pela equação cartesiana
por Neta Silva » Sex Mar 14, 2014 20:58
- 1 Respostas
- 1373 Exibições
- Última mensagem por Russman

Sex Mar 14, 2014 22:43
Introdução à Álgebra Linear
-
- Função de uma variavel (cartesiana, paramétrica e implícita)
por rhmgh » Dom Ago 12, 2012 21:20
- 3 Respostas
- 1801 Exibições
- Última mensagem por MarceloFantini

Qua Ago 15, 2012 10:27
Funções
-
- determinar o valor de K pela equação cartesiana
por Ana Maria da Silva » Seg Set 16, 2013 20:31
- 0 Respostas
- 3762 Exibições
- Última mensagem por Ana Maria da Silva

Seg Set 16, 2013 20:31
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
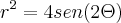

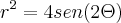


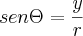

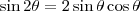 .
.
 e
e 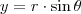 , onde
, onde 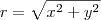 , você encontrará que
, você encontrará que