 por Thays » Sex Jan 20, 2012 14:47
por Thays » Sex Jan 20, 2012 14:47
Sei que to explorano kk mais confere essas outras aqui pra mim:
1)A solução do sistema

é o par ordenado:
R:
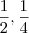
2)A solução da equação

-

é :
R:

3)A raiz da equação 3.(x-5)+1=x-2.(2x-4) sendo

é um numero inteiro:
R: comprendido entre 5 e -5
-
Thays
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sáb Jan 14, 2012 11:26
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso tecnico em Farmacia
- Andamento: cursando
 por Arkanus Darondra » Sex Jan 20, 2012 15:29
por Arkanus Darondra » Sex Jan 20, 2012 15:29
Thays escreveu:1)A solução do sistema

é o par ordenado:
R:
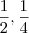
Não. O par é
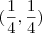
Thays escreveu:2)A solução da equação

-

é :
R:

Por favor, revise o enunciado.
Thays escreveu:3)A raiz da equação 3.(x-5)+1=x-2.(2x-4) sendo

é um numero inteiro:
R: comprendido entre 5 e -5
Não entendi o porque do

Mas para
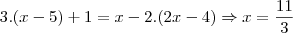
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Thays » Sex Jan 20, 2012 15:48
por Thays » Sex Jan 20, 2012 15:48
1)A solução da equação
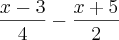
= x é
R:

2)A raiz da equação
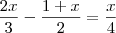
, sendo

é um numero inteiro:
ai tem 4 opções:
a)igual a -5
b)maior que -5
C)menor que -5
d)compreendido entre 5 e -5
-
Thays
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sáb Jan 14, 2012 11:26
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso tecnico em Farmacia
- Andamento: cursando
 por Arkanus Darondra » Sex Jan 20, 2012 16:17
por Arkanus Darondra » Sex Jan 20, 2012 16:17
Thays escreveu:1)A solução da equação
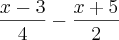
= x é
R:

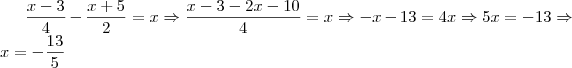
Thays escreveu:2)A raiz da equação
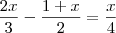
, sendo

é um numero inteiro:
ai tem 4 opções:
a)igual a -5
b)maior que -5
C)menor que -5
d)compreendido entre 5 e -5
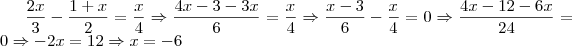
Acho que é a
letra C
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sistemas
por Jansen » Dom Mai 10, 2009 00:01
- 5 Respostas
- 4702 Exibições
- Última mensagem por Molina

Seg Mai 11, 2009 04:36
Sistemas de Equações
-
- sistemas
por Magda » Sex Jun 19, 2009 18:37
- 5 Respostas
- 3745 Exibições
- Última mensagem por Magda

Sex Ago 07, 2009 19:49
Sistemas de Equações
-
- Sistemas...
por GABRIELA » Ter Set 08, 2009 21:41
- 6 Respostas
- 3487 Exibições
- Última mensagem por GABRIELA

Qua Set 09, 2009 18:52
Matrizes e Determinantes
-
- Sistemas
por GABRIELA » Qua Set 09, 2009 18:59
- 2 Respostas
- 1715 Exibições
- Última mensagem por GABRIELA

Qui Set 10, 2009 17:08
Sistemas de Equações
-
- Sistemas
por GABRIELA » Seg Set 21, 2009 17:25
- 4 Respostas
- 2401 Exibições
- Última mensagem por GABRIELA

Ter Set 22, 2009 09:45
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 -
-

 é um numero inteiro:
é um numero inteiro:

 -
-

 é um numero inteiro:
é um numero inteiro:
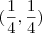
-
é um numero inteiro:

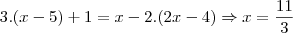

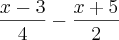 = x é
= x é 
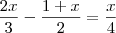 , sendo
, sendo  é um numero inteiro:
é um numero inteiro:
= x é
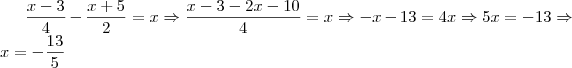
, sendo
é um numero inteiro:
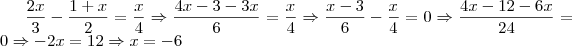



 , avisa que eu resolvo.
, avisa que eu resolvo.

