Descobrir uma medida

por **Andreza** » Qui Jan 19, 2012 11:36

Um marceneiro precisa construir uma esquadria de madeira, conforme as informações:

AB=AC=60cm
BC=3,11cm
BE=3cm
BE perpendicular a AC
CD perpendicular a AB
Qual a medida de CD ?

Fazendo o desenho pude observar q os triangulos entre si sao isosceles, portanto a medidade CD seria igual a medida BC, ou seja, 3,11cm. ( Pelas relações entre congruência e semelhança de triângulos )

Não tenho o gabarito, por este motivo peço a ajuda de vcs para analisar se minha resposta está correta. Desde já estou muito grata.

por **fraol** » Sex Jan 20, 2012 12:59

CD perpendicular a AB
Qual a medida de CD ?

Está faltando mais alguma informação em relação ao ponto D.

por **ant_dii** » Sáb Jan 21, 2012 03:35

: um desenho possível; esquadria2.png.jpg (5.91 KiB) Exibido 1804 vezes

Bom, esse foi um possível desenho, mas com as informações que deu...
eu encontrei como resposta para $\overline{CD}$ , 3 e não 3,11...
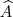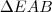Para isso observei que o ângulo $\widehat{A}$ é comum aos triângulos $\Delta CAD$ e $\Delta EAB$ , e ambos possuem um ângulo reto, por isso são semelhantes...
daí que $\frac{AB}{AC}=\frac{CD}{EB} \Rightarrow 1=\frac{CD}{3} \Rightarrow CD=3$ ...

Descobrir uma medida

Descobrir uma medida

Descobrir uma medida

Re: Descobrir uma medida

Re: Descobrir uma medida

Quem está online