Olá Miguel.
Seja bem-vindo. Todas as dúvidas são importantes.
Vamos resolver os problemas utilizando as palavras como variáveis para facilitar o entendimento, com o seguinte significado:
Maria: fração da pizza comida pela Maria
Rui: fração da pizza comida pelo Rui
Comeram: fração total da pizza comida
Sobra: fração que sobrou da pizza
Maria =

Rui =

Repare que palavra "guloso" sugere que o Rui comeu mais.
De fato, pois
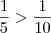
.
Veja que em frações, fixando o numerador, quanto mais o denominador aumenta, menor fica a fração.
Comeram = Maria + Rui
Comeram =
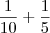
Aqui, para somarmos as frações, precisaremos deixá-las com um denominador comum, é o chamado M.M.C. (mínimo múltiplo comum). Ou seja, o M.M.C. é o menor número que é múltiplo dos dois denominadores, simultaneamente.
Você deve lembrar do algoritmo para obtenção, de qualquer forma, esta é a idéia:

Você tenta iniciar uma divisão por 2, por 3 e assim sucessivamente, colocando os resultados nas colunas 1 e 2.
A coluna 3 é o número pelo qual algum denominador foi dividido.
Quando por fim você obtiver 1 como resultado nas colunas 1 e 2, calcule o produto dos valores da coluna 3, este será o M.M.C..
Voltando, neste caso então, começamos colocando o M.M.C. encontrado como denominador das frações:
Comeram =

Comeram =
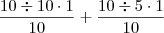
Comeram =
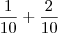
Agora podemos somar os numeradores, pois o denominador é comum.
Comeram =
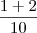
Comeram =

Por fim, vamos calcular a sobra.
Antes, note que a pizza inteira equivale a uma unidade, portanto:
Sobra = 1 - Comeram
Sobra = 1 -

Sobra =
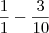
Devemos calcular também o M.M.C. entre 1 e 10 que é

, veja:
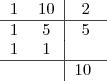
Sobra =
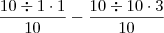
Sobra =

Sobra =
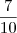
Note que se você somar o que comeram com a sobra, deverá obter 1 (que é a pizza toda), veja:
Comeram + Sobra =
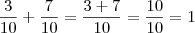
A intenção aqui está muito distante de explicar M.M.C. ou o entendimento do algoritmo.
Estes seriam outros problemas.
Por outro lado, foi apenas uma descrição do procedimento prático.
Espero ter ajudado!




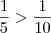 .
.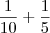


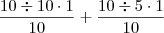
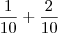
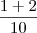

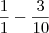
 , veja:
, veja: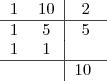
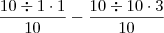

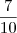
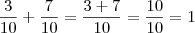



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.