 por Renato_RJ » Sex Jan 13, 2012 19:44
por Renato_RJ » Sex Jan 13, 2012 19:44
Boa noite amigos !!!
Gostaria que alguém me ajudasse com uma função, na verdade não quero a solução do problema, só quero entender como "lidar" com a questão abaixo.
![[\frac{2x^2}{x^2+1}] = x [\frac{2x^2}{x^2+1}] = x](/latexrender/pictures/be586c672c5b5ab35fde1eb5df6f4362.png)
Onde
![[x] [x]](/latexrender/pictures/3e5314e9fd31509fdeb83faa0f729ba2.png)
é o menor inteiro maior ou igual a x.
E aí está a minha dúvida, posso lidar com essa equação como uma equação "normal" ou tem algum detalhe que não sei ??? Mais uma vez muito obrigado, não precisa resolver o problema só quero "o caminho das pedras"...
[ ]'s
Renato.
EDITADO:
Na verdade o nome dessa função é função teto, então a equação seria:
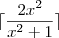
Acho que consigo fazer algum progresso agora..
EDITADO 2:
Esqueçam, já resolvi !!!

Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por ant_dii » Sáb Jan 14, 2012 02:31
por ant_dii » Sáb Jan 14, 2012 02:31
Mas agora eu me interessei... kkkkk
Poste, por favor se não for incomodo, o que você fez...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Renato_RJ » Sáb Jan 14, 2012 12:12
por Renato_RJ » Sáb Jan 14, 2012 12:12
Simplesmente desenhei o gráfico de ambas as funções e vi onde eles se interceptavam, só achei três valores onde elas se interceptam que são 0, 1 e 2...
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por ant_dii » Sáb Jan 14, 2012 15:42
por ant_dii » Sáb Jan 14, 2012 15:42
Pesquisei sobre o tema e descobri que pouco se fala sobre esta função...
Mas eu mesmo fiquei com muitas dúvidas, por exemplo, como confirmar que só existe esses três pontos? E se fosse igual à

, qual seria o resultado? Como confirmá-lo? Como fazer isso algebricamente?
Ela é muito interessante...
Fui procurar respostas e percebi que para responder tais questões é preciso estudar o comportamento do gráfico da função teto (o recurso que você utilizou) utilizando máximos e mínimos da função e qual é o comportamento dela no infinito (

) ou quando se aproxima de zero, ou seja, utilizando limite e somente depois fazer a intersecção com a função desejada. Isso porque é difícil saber o comportamento da função que você postou.
De outra forma, mas agora analítica, pode-se fazer o seguinte também.
Considerando que
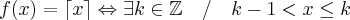
, teremos
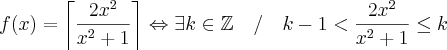
de onde
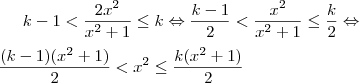
.
Agora, de
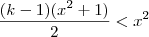
, temos
.
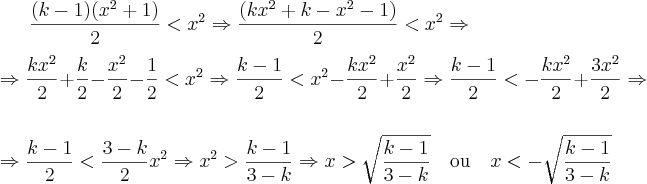
Se

, teremos
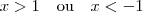
.
de
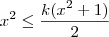
, teremos

.
Se

, então

.
Se

, então
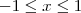
.
assim podemos ver que
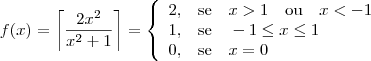
Agora é possível fazer a intersecção da função

com a função
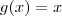
.
Que retorna os pontos

,

e

.
Se fosse com a função
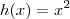
, os pontos seriam

,
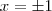
.
Fiz isso só por curiosidade... Mas obrigadoo
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Renato_RJ » Sáb Jan 14, 2012 18:06
por Renato_RJ » Sáb Jan 14, 2012 18:06
Cara, eu que te agradeço !!!
Agora sei como funciona analiticamente....
Muito grato mesmo...
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Pequena dúvida
por Fernanda Lauton » Sáb Jul 03, 2010 22:53
- 4 Respostas
- 2457 Exibições
- Última mensagem por Fernanda Lauton

Seg Jul 05, 2010 13:37
Logaritmos
-
- Potência - Pequena dúvida
por CaioCaesar » Seg Abr 16, 2012 07:14
- 1 Respostas
- 1432 Exibições
- Última mensagem por jacobi

Qua Abr 18, 2012 10:43
Álgebra Elementar
-
- sistema de equações do 2º grau pequena dúvida
por TAE » Sex Jun 08, 2012 20:24
- 1 Respostas
- 2023 Exibições
- Última mensagem por Molina

Sáb Jun 09, 2012 14:37
Sistemas de Equações
-
- Tamanho da amostra - população heterogenia e pequena
por Roniberto » Sex Fev 13, 2009 15:41
- 2 Respostas
- 2872 Exibições
- Última mensagem por Roniberto

Ter Fev 17, 2009 09:22
Estatística
-
- Pequena ajuda de "arranque"!
por eicma » Sex Dez 11, 2009 14:29
- 0 Respostas
- 991 Exibições
- Última mensagem por eicma

Sex Dez 11, 2009 14:29
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![[\frac{2x^2}{x^2+1}] = x [\frac{2x^2}{x^2+1}] = x](/latexrender/pictures/be586c672c5b5ab35fde1eb5df6f4362.png)
![[x] [x]](/latexrender/pictures/3e5314e9fd31509fdeb83faa0f729ba2.png) é o menor inteiro maior ou igual a x.
é o menor inteiro maior ou igual a x.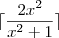


 , qual seria o resultado? Como confirmá-lo? Como fazer isso algebricamente?
, qual seria o resultado? Como confirmá-lo? Como fazer isso algebricamente? ) ou quando se aproxima de zero, ou seja, utilizando limite e somente depois fazer a intersecção com a função desejada. Isso porque é difícil saber o comportamento da função que você postou.
) ou quando se aproxima de zero, ou seja, utilizando limite e somente depois fazer a intersecção com a função desejada. Isso porque é difícil saber o comportamento da função que você postou.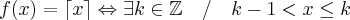 , teremos
, teremos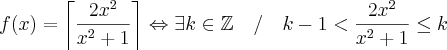
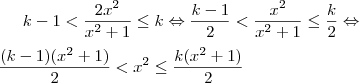 .
.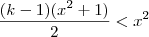 , temos
, temos .
. , teremos
, teremos 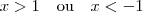 .
.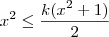 , teremos
, teremos .
. , então
, então  .
. , então
, então 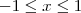 .
.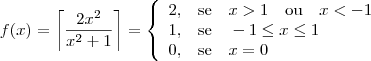
 com a função
com a função 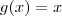 .
. e
e  .
.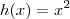 , os pontos seriam
, os pontos seriam 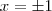 .
.