 por anniewallker » Sex Jan 13, 2012 14:19
por anniewallker » Sex Jan 13, 2012 14:19
Boa tarde pessoas,
Eu to com uma super duvida
eu tenho uma questão que, é simples,mas meu cérebro tah travado não to conseguindo desenvolver.
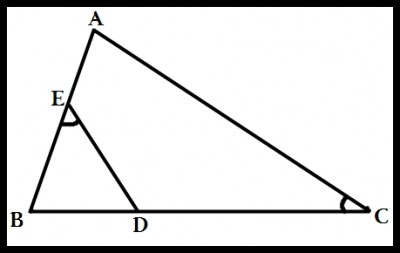
No triângulo ABC, temos AB= 8 cm, AC = 10 cm, BD = 2 cm e BE = 4 cm. Sabendo que os ângulos ACB e BDE têm medidas iguais, então o perímetro do triângulo BDE é:
a) 6,5 cm
b) 7,0 cm
c> 5,5 cm
d) 8,0 cm
E) 8,5 cm
imagem do triângulo em anexo.
Alguém pode me ajudar??
Por favor?
desde já agradeço
bjux
- Anexos
-
-
anniewallker
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jan 11, 2012 23:02
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informática
- Andamento: formado
 por DanielRJ » Sex Jan 13, 2012 17:39
por DanielRJ » Sex Jan 13, 2012 17:39
Achei perimetro 11 cm.
Colocando o angulo do enunciado pq na imagem ta contrario do enunciado.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por anniewallker » Sex Jan 13, 2012 17:45
por anniewallker » Sex Jan 13, 2012 17:45
DanielRJ escreveu:Achei perimetro 11 cm.
Colocando o angulo do enunciado pq na imagem ta contrario do enunciado.
Daniel mas é assim mesmo que está a questão :(
-
anniewallker
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jan 11, 2012 23:02
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informática
- Andamento: formado
 por anniewallker » Sex Jan 13, 2012 19:37
por anniewallker » Sex Jan 13, 2012 19:37
DanielRJ escreveu:O enunciado da errado o angulo congruente seria BÊD
conforme a imagem achei resposta 8,5 cm postarei o anexo

Brigadão Daniel!!!
tirou o pai da forca *-*

-
anniewallker
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jan 11, 2012 23:02
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informática
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Semelhança
por TAE » Qui Jun 21, 2012 23:10
- 5 Respostas
- 5366 Exibições
- Última mensagem por TAE

Ter Jun 26, 2012 22:02
Geometria Plana
-
- Semelhança
por TAE » Ter Jul 03, 2012 20:14
- 4 Respostas
- 1975 Exibições
- Última mensagem por TAE

Qui Jul 05, 2012 20:28
Geometria Plana
-
- Semelhança de triangulos
 por DanielRJ » Ter Dez 28, 2010 19:30
por DanielRJ » Ter Dez 28, 2010 19:30
- 7 Respostas
- 5486 Exibições
- Última mensagem por Otavio Rubiao

Qui Jan 27, 2011 10:36
Geometria Plana
-
- Semelhança de triângulos
 por igorcamilo » Sáb Jun 04, 2011 19:55
por igorcamilo » Sáb Jun 04, 2011 19:55
- 1 Respostas
- 2443 Exibições
- Última mensagem por Adriano Tavares

Dom Jan 01, 2012 14:55
Geometria Plana
-
- Semelhança de triângulos
por Gaussiano » Sáb Dez 10, 2011 13:59
- 0 Respostas
- 1588 Exibições
- Última mensagem por Gaussiano

Sáb Dez 10, 2011 13:59
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




