 por Raphael Feitas10 » Sex Jan 13, 2012 02:23
por Raphael Feitas10 » Sex Jan 13, 2012 02:23
Um trem parte de uma estação com certo numero de passageiros.Na primeria parada, saltaram 3/7 do numero de passageiros e na estação seguinte entraram 40.Na penúltima estação sataram 5/8 dos passageiros.Calcule com quantos passageiros ele saiu da estação inicial,sabendo que chegou à estação final com 36 passageiros. R: 98 passageiros
Brother eu fiz desse jeito aqui por equação mais ñ obtive êxito
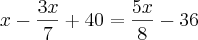
tentei fazer pelo raciocínio só de fração mais ñ conseguie tbm me ajuda aew desde de ja muito agradecido...
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por ant_dii » Sex Jan 13, 2012 03:18
por ant_dii » Sex Jan 13, 2012 03:18
Na verdade você estava no caminho certo, mas veja que quando saltaram na penúltima parada, a contagem é feita em cima dos que haviam sobrado da primeira estação mais os 40 que entraram na segunda, ou seja, 5/8 desse total.
Assim sua conta ficará:

passageiros depois da segunda parada.
Supondo que não houve paradas depois da segunda até a penúltima estação, e considerando que nesta parada desceram 5/8 dos passageiros, teremos
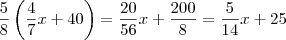
.
Assim, teremos

resolvendo você encontrará o resultado correto.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Fração] Ajuda em problema de fração.
por smlspirit » Sex Mai 18, 2012 01:17
- 3 Respostas
- 3797 Exibições
- Última mensagem por DanielFerreira

Dom Mai 20, 2012 17:06
Álgebra Elementar
-
- fração
por leandro moraes » Qui Jan 14, 2010 19:41
- 1 Respostas
- 1685 Exibições
- Última mensagem por MarceloFantini

Qui Jan 14, 2010 20:09
Estatística
-
- Fração
por bia rosendo » Seg Jun 06, 2011 11:45
- 2 Respostas
- 4504 Exibições
- Última mensagem por Claudin

Seg Jun 06, 2011 18:34
Matemática Financeira
-
- Fração 110
por Raphael Feitas10 » Seg Jan 09, 2012 17:28
- 1 Respostas
- 1842 Exibições
- Última mensagem por Arkanus Darondra

Seg Jan 09, 2012 18:43
Sistemas de Equações
-
- Fracão
por Yasmin Felix » Sáb Jan 14, 2012 13:34
- 3 Respostas
- 2160 Exibições
- Última mensagem por marques_gc

Sáb Jan 14, 2012 14:14
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
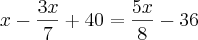 tentei fazer pelo raciocínio só de fração mais ñ conseguie tbm me ajuda aew desde de ja muito agradecido...
tentei fazer pelo raciocínio só de fração mais ñ conseguie tbm me ajuda aew desde de ja muito agradecido...
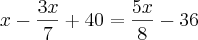 tentei fazer pelo raciocínio só de fração mais ñ conseguie tbm me ajuda aew desde de ja muito agradecido...
tentei fazer pelo raciocínio só de fração mais ñ conseguie tbm me ajuda aew desde de ja muito agradecido...
 passageiros depois da segunda parada.
passageiros depois da segunda parada.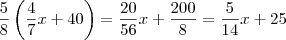 .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.